José María Cordero Larriera

 

 

 

 

 

 

 

 

 

 

        COMPLEJIDAD Y ESPECIFICIDAD

 

                         

 

 

                                 EN

           

 

 

 

                  SISTEMAS BIOLOGICOS

 

 

 

 

 

 

                                                           

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Sorin Comorosan

 

 

Grupo Interdisciplinario de Investigación-

Departamento de Post Grado – Bioquímica-

Fundeni Hospital

Bucaresti

 RUMANIA

 

 

 

 

José María Cordero Larriera

 

Biomatemática – Departamento de Matemática –

Facultad  de  Ciencias Exactas  y  Naturales –

Departamento De Física – Laboratorio Electrónica Cuántica –

Universidad de Buenos Aires - Integrante del Consejo Nacional de

Investigaciones Científicas y Técnicas

ARGENTINA

 

 

 

 

                                                   ABRIL 2004

 

 

  

 

 

 

COMPLEJIDAD Y ESPECIFICIDAD EN SISTEMAS BIOLOGICOS

 

 

 

 

Cuando las matemáticas se usan para modelar a los sistemas biológicos,  una serie de dificultades son encontradas de inmediato. Entre ellas, la complejidad  de los sistemas considerados, aparece como la más importante. Cuando se trata a la complejidad biológica la mayoría de los modelos matemáticos que fueron usados hasta hoy han tenido desafortunadamente poca relevancia científica. Como los teóricos del dominio de las ciencias exactas dicen,  la biología teórica  describió, si no de una manera mas elegante pero, muy bien conocida y útil para los biólogos.

Nosotros creemos que hay dos razones para esta situación:

 

Los modelos matemáticos no tienen, en principio el poder de predecir, ya que  no son teorías. Esos modelos son diseñados para “imitar” la realidad y haciéndolo, permiten observar o describir más claramente alguna de sus características. Las teorías son construidas en forma diferente:

 

Axiomas, proposiciones, reglas, se usan para construir teoremas con los cuales, algunas veces (pero no muy habitualmente) aspectos nuevos de la realidad son inferidos. El éxito poco común de la teoría de catástrofes de Rene Thom en predecir la aparición de formas biológicas  (morfos)  es un ejemplo relevante. Esto no quiere decir  que no hay modelos matemáticos con profunda relevancia científica en biología. Robert Rosen, usando la matemática de la teoría de códigos construyo un modelo matemático que requirió la necesidad de un mensajero inverso en el código genético, en los albores de la biología molecular. Este componente biológico (una enzima) fue descubierto años mas tarde, por casualidad.

COMPLEJIDAD   es otro concepto pobremente comprendido. La palabra tiene más de un sentido y definitivamente uno muy particular. En física los sistemas complejos aparecen desde el número de sus componentes. Entonces, la matemática usada, es la del  “número”, las leyes  del conjunto de números y las diferentes características de los números fueron creadas para este estudio. En biología esto no es así. El número de los componentes de un sistema no induce  necesariamente la complejidad.   Son las relaciones entre ellos que en general inducen a esto. En tanto que la física es número, en biología es geometría y topología.

 

 Para discutir  complejidad y especificidad que se vincula a la biología, nosotros  tenemos primero que hacer una serie de definiciones básicas con respecto a los sistemas y sus propiedades.

La palabra sistema también ha sido usada en una variedad de contextos, frecuentemente no bien definidos, induciendo a muchas confusiones.

 

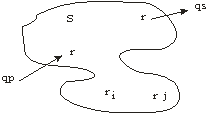
DEFINICION 1: Un sistema  es una parte bien definida de lo real. Esta constituido por un número finito ( ri j , i j = 1,….,n)  interactuando  dentro de los limites del sistema  e interactuando con un número finito de componentes ( q p s  , ps = 1,…,n) fuera de los limites del sistema.

S ( ri j , i , j ,  j= 1,…..,n) )    , ( q p s  , p , s= 1,….,n)

 

FIGURA 1: Definición de un sistema

 

 

 

 

 

 

PROPOSICION 1: La propiedad de un sistema es una noción primaria.

 

Dos comentarios de naturaleza filosófica son apropiados en este desarrollo.

 

Nuestra definición de un sistema es una definición dinámica (funcional). En principio un sistema real no puede ser completamente aislado del mundo real. Entonces, un sistema es una parte de la realidad, y no una cantidad indefinida de ella.

 

La elección de la propiedad como noción primaria, tiene severas limitaciones, indicando claramente que nosotros  no vamos a entender  que es realmente una propiedad. Pero, nosotros podemos usar la propiedad como criterios  para discutir sistemas, entonces conseguiremos un alto nivel de rigor en nuestras discusiones.

 

PROPOSICION 2 :  Si nosotros introducimos en el conjunto de sistemas { S } una relación de orden ( > ) relativa a una propiedad ordenada como  p, ( >p ), entonces el conjunto del sistema { S } viene  a ser un conjunto ordenado ( { S } , >p ). Como el conjunto de los números es también un conjunto ordenado ( , ≥) nosotros podemos definir una aplicación (f) entre dos componentes

                                                 

                                                  fp  : { S } →                             (1)

 

con la condición

                                             S1 >p  S 2  f p   (S2)                         ( 2 )

 

Entonces nosotros podemos decir que la aplicación f p  determina una  medida   del sistema S, con respecto a la propiedad ordenada p. En física f p  se llama observable.

 

 

PROPOSICION 3: Tiene un profundo significado, implica que nosotros podemos medir propiedades (que no son definidas directamente ), dentro de una estructura de una relación de orden, esto implica también que nosotros  podemos establecer conexiones, que son      , (correspondencias o aplicaciones) entre las propiedades del sistema que fueron formalizadas por la aplicación  fp .  Observamos que la aplicación de tipo f p  vincula la  “propiedad “de un sistema al conjunto de números  , es decir a los números. Ya que el cardinal  de   es א , esto nos dice  que nosotros podemos describir conexiones en sistemas finitos de componentes y todo esto nos permitió  introducir  la tercera proposición.

 

PROPOSICION 4: La complejidad física aparece por la interacción de un largo numero de los componentes del sistema, con respecto a mas de una propiedad de orden (>). En física complejidad representa propiedades ordenadas. Ya que cualquier sistema biológico puede ser reducido (por lo menos en principio) en nivel básico (y solo en este nivel) en un sistema físico, esto significa que la complejidad biológica comienza en la física.

 

PROPOSICION 5: El primer nivel de complejidad biológica es la complejidad física también. Vamos ahora a describir matemáticamente (como ejemplo)  la mas general de las propiedades de un sistema físico y mostrar, acorde a la proposición  (4) como la complejidad física aflora por la interacción de los componentes del sistema con respecto a estas propiedades. Formalmente podemos nosotros  representar la energía interna de un sistema físico U, como una función de la entropía, volumen, numero de partículas, carga eléctrica, magnetismo y área:

                                                                                                                

                                                U = μ (S, v, N,  M , A)                                  (3)

 

El modelo matemático que relaciona estos componentes, es llamado en física el PRIMER PRINCIPIO DE LA TERMODINAMICA

 

 

 

 

 

 

                                                                                                                                           

                                dU  =  T dS – P dV +  μ dN + Ø dq +  H dM + dA        (4)

 

Este modelo es tan real como puede serlo y, fenomenológicamente con un profundo poder de descripción  (derivado de un real «  comportamiento »). Sea como primera observación  que nuestro sistema posee propiedades globales (que son invariantes a través de todo el sistema) como el número de partículas, volumen, área, propiedades locales (variando a través del sistema) como temperatura, presión, potencial químico. El modelo (4) vincula las propiedades globales con las locales y describe la realidad que resulta de esta vinculación.

 

  PROPIEDAD GLOBAL            PROPIEDAD LOCAL      REALIDAD RESULTANTE

 

                     S                                T                                          Desorden  

                     V                                P                                          Trabajo mecánico

                     N                                μ   (Potencial Químico)       Reacciones Químicas

                     q                                Ø  (Potencial Eléctrico)       Trabajo Eléctrico

                                                     

                     M                               H (Campo Magnético)        Trabajo Magnético

                      A                               Γ (Tensión superficial)        Elasticidad

 

FIGURA 2: Relaciones entre propiedades locales y globales

                     de un sistema físico, modelado por una ecuación.

 

Es menester hacer un comentario sobre el modelado (4) que es una ecuación diferencial. Es necesario usar  derivadas ya que los modelos científicos son dinámicos y la única manera que nosotros conocemos para describir de una forma consistente las variaciones es por la derivación, ya que la  fuerza es una derivada segunda, no hay más que aplicarla  cuando se habla de dinámica, fuera de este formalismo. Ahora la represtación geométrica de la derivada de una función es una curva, esto es un recorrido en el espacio y el tiempo.

Esto nos dice que la dinámica es una interacción entre recorridos y nada más que eso, pero esto es una gran limitación de todas las dinámicas de modelos que usan derivadas.  Es, pensamos una de las razones del por que las dinámicas de los procesos biológicos modelados como fueron mencionados, han tenido tan poca relevancia. Por que en biología no es significativo el recorrido que cambia con el tiempo, pero en una superficie que abarca un volumen si. Consecuentemente los instrumentos matemáticos de significación son: las integrales, la geometría diferencial y la topografía diferencial.

 

Sea ahora la posibilidad de discutir modelando matemáticamente los sistemas físicos (i, e: sistemas reales) con muchos componentes  interactuando entre las propiedades de estos componentes vinculados con la PROPOSICION 4. Sea un modelo  F    experimental (i. e.: factores) que pertenecen a la realidad y que introduce las siguientes operaciones entre ellos.

    

                1.- AB pertenece a la realidad si A y B pertenecen a la realidad.

                2.- A  B si un experimento A es implicado por el experimento B.

                3.- Ø es el conjunto vació, esto es que los factores experimentales no ocurren.

 

Esta claro,  nosotros estructuraremos a F   como un conjunto de filtro lógico

Sea ahora considerada una teoría matemática M, conteniendo axiomas y teoremas.

                                       a, b, c,……………. M

Nosotros llamaremos una representación del conjunto experimental F    con el modelo matemático M. A cualquier función

                                                     r: M → F                                     (5)

 De manera que r (M) F    sea una base para el conjunto filtrado F  y es obvio que M

es también un conjunto filtrado lógicamente, el núcleo de este filtro es el conjunto de todos los axiomas,  A  M   P (M)  es claro que, con este formalismo nosotros ahora podemos comparar modelos matemáticos y como consecuencia las representaciones.

 

 

 

 

PROPOSICION 6: Un modelo matemático M1  es mas fuerte que M2  si

 

                                                   r(A  M1) A  M2                          (6)

 

(i.e.: una parte de los axiomas de A  M2  se transforman en teoremas en M1)

                                                r

                     M1→  r → M2  

modelo del modelo.

                             A  M1  P  (M1)       A  M2   P   (M2)     M  F

FIGURA 4: Relaciones entre modelos matemáticos.

 

Aplicaremos ahora este formulismo al modelo  (4).

Consideremos para mas claridad solo la parte de este modelo, por ejemplo gases a baja presión. Sea  F  en este contexto el conjunto de todos los experimentos con respecto a este sistema particular, entonces nosotros tenemos las siguiente relaciones entre las diferentes representaciones.

                           F                                                                         Resultados experimentales

                            M1    PV= constante. (si T = constante)----------------------------↑

                           M2   PV=NkT------------ ↑            Termodinámica

                           M3   z= e-H//KT   dp         dr,              F= kT ln z, P=-F/T estadística

                                                        ↑            ↑                            

                           M4  Axioma      w=0       ↑

                           M5  Estadística matemática----------- ↑

 

 

FIGURA7: Modelado de niveles.

 

 

 

 

 

 COMPLEJIDAD BIOLOGICA

Es lo que discutiremos ahora:

 

PROPOSICION 7: La Complejidad Biológica aparece de la interacción de los componentes del sistema que genera nuevas propiedades. Queda inmediatamente claro que la definición (7) vincula la complejidad con un orden jerárquico y con niveles jerárquicos, esto es la teoría de jerarquía. Ahora naturalmente el problema es como  tratar matemáticamente las estructuras jerárquicas. Con la  naturaleza se  enlaza  la posibilidad de abordar matemáticamente las estructuras jerárquicas. En nuestra opinión este es un problema profundo y difícil que puede reducirse a su más simple forma, las relaciones (para cualquier situación particular y compleja de la biología) entre los niveles de descripción y niveles de estructura .Indudablemente este es también un profundo problema filosófico, i. e.  la naturaleza de los isomorfismos, que vinculan nuestras representaciones a realidades particulares, y  que estos isomorfismos son supuestamente la representación.

 

Niveles de descripción: El tipo general de descripción usado en física (y en las llamadas ciencias exactas) derivan de un principio muy profundo y fuertemente sostenido: la estructura a ser descripta es supuestamente aislada largamente de su descripción y absolutamente sin influencia o control. Esto es el corazón de la teoría de los sistemas dinámicos. Esta situación extrema tiene unos contra argumentos, derivados desde la mecánica quántica, este es el principio de incertidumbre de Heisemberg, que nos permite un indeterminismo necesario en algunas descripciones de dinámica compleja, cuando nosotros tendemos a observar o controlar eso. El tipo de descripción generalmente usado en sistemas simbólicos  o lógicos presentes, de manera interesante, es exactamente la misma situación. La descripción también deriva de un principio fuerte: la estructura a ser descripta se asume que esta completamente subordinada a su descripción. Esto es el corazón de Inteligencia Artificial.

Teoría y Modelos. Esta situación tuvo su contra argumento, derivado de la naturaleza, este es el teorema de incompletitud de Gödel, que permite por símbolos y operaciones de lógica que son completamente precisos y determinísticos, generar problemas insalvables. Y esto nos conduce al esencial paralelismo Herziano, cualquier descripción que nosotros podamos elegir para tratar cualquier no materia, parte de la realidad: la consecuencia de la  descripción debe describir consecuencias de los eventos naturales. En este contexto observamos que las descripciones matemáticas tienden a crear descomposiciones totales, de manera que los niveles de jerarquía aparecen totalmente aislados unos de otros. Con esto llegamos aun importante teorema, con singulares implicancias filosóficas: 

Teorema de descomposiciones de sistemas ( Mesarowicz)

De cualquier manera que nosotros descompongamos un sistema, la información contenida en los subsistemas resultantes es siempre menor que la información contenida inicialmente en el sistema original. Esto finalmente nos lleva al aspecto significativo concerniente a las descripciones matemáticas de la complejidad biológica: para analizar un sistema biológico complejo debemos de diseñar una teoría jerárquica formulada para describir un mismo y mínimo de dos niveles simultáneamente, el nivel de la estructura y el nivel jerárquico induciendo la nueva propiedad. En otras palabras en biología es necesaria una matemática de descomposición parcial.

Niveles de Estructura: Una de las más significativas y fascinantes propiedades generadas por las estructuras biológicas es la especificidad. En el  sentido más general la especificidad representa una interacción restringida de un número rigurosamente fijado de grados de libertad. Naturalmente en este sentido la mayoría de las reacciones químicas son específicas.

 

PROPOSICION 8: El primer nivel de especificidad biológica es la química. En biología la especificidad esta en primer lugar, es la geometría y con respecto a esto, “mas“geometría inducirá y conseguirá mas especificidad

Entonces el primer nivel de la especificidad, la química es el resultado de las formas básicas de los orbítales quienes determinan las interacciones químicas. La especificidad es geometría a nivel microscópico. El siguiente nivel de especificidad aparece con las estructuras súper moleculares. Discutiremos ahora un ejemplo representativo de un nivel jerárquico bajo. La molécula de glucosa tiene una especificidad muy estricta con respecto a su enzima que la corta que se llama glucoxidasa. La molécula de galactosa tiene una especificidad muy baja (10% de la glucosa) con respecto a la misma enzima, a pesar que la estructura química es idéntica. Solo la geometría es ligeramente diferente, en una sola posición  OH,  y esta posición no es implicada en la unión de la molécula y la enzima.

Un ejemplo representativo para un nivel jerárquico es provisto por la estructura de la proteína. Las proteínas son moléculas complejas, formadas por aproximadamente 20 componentes diferentes de (aminoácidos y ácidos). El primer nivel de la jerarquía es representado por la asociación lineal de estos elementos. La cadena resultante (llamada polipéptido) presenta una serie de interacciones específicas que pueden derivar con facilidad de la especificidad química del nivel inferior (aminoácido). A un nivel más alto las cadenas  se asocian en redes que son representadas en una geometría  bidimensional. Las proteínas que resultan llamadas, lineales, presentan interacciones específicas que pueden ser analizadas dentro del contexto de las uniones químicas entre regiones diferentes de cadenas polipéptida. A un tercer nivel las cadenas forman estructuras globulares con una bien definida química de la superficie exterior y una bien definida  superficie exterior. La geometría de una estructura globular genera interacciones biológicas específicas de naturaleza inmunológicas. A un cuarto nivel jerárquico las estructuras globulares se asocian en unidades complejas (llamadas monómeros) de diferente multiplicidades.

El número de las unidades diferentes y la geometría de sus asociaciones inducen altos niveles de interacciones específicas que se reflejan en diferentes patters de cinética.

Nosotros concluimos que la especificidad biológica es geometría al nivel microscópico.

 

 

 

 

 

 

 

 

 

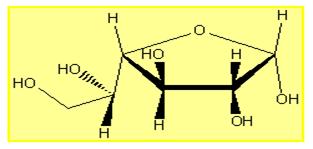
 La galactosa en otra forma de expresión

 

 

 

 

 

 

FIGURA 6: Otro ejemplo de la especificidad biológica inducida tras una ligera diferencia

                     en un grupo químico.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 FIGURA 9: Un grado mas elevado  de especificidad y complejidad

 

 

        

 

 

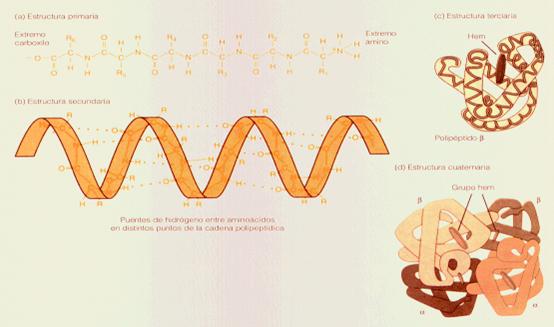
FIGURA 10: Mas especificidad y complejidad .