E L E F E
C T O C O N T I N U O P E R IO D I C O
P R
O D U C I D O P O R IR R A D 1 A C 1 0 N
C 0 N B A
J A S E N E R G I A S•••
&
LA TEORIA ALGEBRAICA DE LOS
PROCESOS RELACIONALES •••
C. A.
Leguizamón
A. N.
Zaretzky
J. M. CORDERO LARRIERA
M. A. ALEGNANI
••••
1989
RESUMEN
La teoría algebraica de los Procesos relacionales constituye
una argumentaci6n nueva dentro de la Biología Relacional, que ha llevado a
nuevas definiciones matemáticas, a explicaciones relacionales de los procesos
biol6gicos y al descubrimiento del Efecto Continuo Peri6dico sobre la Materia.
Este trabajo muestra tres tipos distintos de investigaciones relacionados con
la teoría: la definici6n de un nuevo reticulado, el Reticulado de la Flecha
Heyting y el hallazgo de teoremas relacionados con éste; la obtenci6n del
álgebra correspondiente a la interacci6n antígeno anticuerpo por medio de la
teoría relacional; y la reiteraci6n del, Efecto Continuo Peri6dico sobre el
crecimiento de plántulas de trigo por irradiaci6n con bajas energías de un
nutriente especifico.
INTRODUCCION
La Biología Relacional comenz6 con los trabajos de J.‑H.Woodger
(1937) y ha sido principalmente desarrollada por N. Rashevsky a partir del año
1954 y hasta 1972. Otros autores, sobre las bases de Rashevsky, también han
contribuido al desarrollo de esta rama de la Biomatemática: Rosen (1958a,1958b
y 1972), Baianu (1970,1971,1980), Baianu y larinescu‑ (19(158), Bvaianu Y
Serircariu (1973), Comorosan y Baianu (l9ó9), Arbib (1966), Demetrius (lq66),
?oster (1966).
La Biología Relacional considera compartimientos cualitativos
en los sistemas, interpretando a éstos en términos de propiedades funcionales.
El Principio de invarianza Relacional de N. Rashevsky,
expresa que los organismos se relacionan a través de sus propiedades naturales
P de tal manera que una organizaci6n funcional del tipo

 Ps Pc Pm
Ps Pc Pm
(s: sensitividad al estímulo, c: conducci6n del estímulo;
m: movimiento ordenado)
dada en organismos primordiales es mantenida a través de
todo el conjunto de sistemas biológicos, determinando similares dígrafos entre
subpropiedades de estos últimos. Obsérvese que una misma propiedad funcional
puede tener lugar en distintos sistemas, a través de mecanismos físico‑químicos
completamente distintos. También, las propiedades funciona les se manifiestan a
niveles jerárquicos distintos en un mismo sistema. Esto significa que todas las
manifestaciones cuantitativas en Biología son debidas a una organizaci6n
subyacente, de tipo cualitativo, cuya constancia a través de los sistemas
identifica por sí a la misma Biología. La teoría algebraica de los procesos
relacionales comenz6 a desarrollarse a partir La teoría relacional se fue desarrollando
a través de la búsqueda de condiciones sobre los dos conceptos relacionales
obtenidos. Simultáneamente, los nuevos conceptos permitieron inferir nuevas
estructuras relacionales. En categorías, lo que mejoro la interpretaci6n de los
sistemas relaciónales. Así, fue aplicado el Lema de Yoneda (Leguizam6n 1976)
descubriéndose que objetos del tipo
1 X 2 x
? Ej 2 , J={1, 1, …,n-1 }
j J
J
que expresaban salidas exclusivamente energéticas del tipo ρB
de la figura 1.l., eran debidas a ingresos adicionales al sistema.
Las energías extrínsecas fueron reconocidas a través de
cinco condiciones, las que siendo definidas a partir del trabajo de 1975, se
completaron en Leguizam6n (1982). Este concepto relacional definía una energía
inherente a su naturaleza física material, con la posibilidad de más de un
valor de energía extrínseca ligada a la anterior, no necesariamente constante
el número de energías ligadas, (y por lo tanto de característica lábil en la
unión) y además, con la posibilidad de continuidad entre distintos valores de
energía que pueden ligarse a la naturaleza física material.
De hecho, estas condiciones se corresponden para un rango de
bajos valores de energía en relación al valor de energía equivalente al de la
naturaleza física material.
Leguizam6n, en su trabajo de 1982, reiter6 que ingresos
adicionales de energía extrínseca E x 0 que se ligasen
a un producto de ingresos originales
X
x 11 E x1 ic‑ J 1 (J = t 1,2, .... n‑11 )
podían dar lugar a un nuevo tipo de salidas del sistema.
Estos criterios interpretados por medio de la figura 1.3.
 X 1 X2
X 1 X2
x
 ? Ex 1 } E1
2
? Ex 1 } E1
2
x En-12
Ex 0
FIGURA 1.3.
sugieren que una variaci6n continua de los valores de
energía extrínseca Ex 0 ligados al ingreso original X1
x ? Ex 1 será correspondida por una respuesta expresada
por la variaci6n continua en el rango, como se tendría para la cardinalidad de
X21 x
? Ej 2
j J
J
Esto ultimo constituy6 el Principal descubrimiento te6rico
obtenido a partir de los desarrollos relacionales. Esto fue verificado
experimentalmente por medio de irradiaciones con bajas energías (λ=546 nm,
I = 3350 lux) durante tiempos del orden de los segundos, efectuadas sobre un
muy conocido revelador fotográfico, el Parametil aminofenol sulfato (metol) en
estado s6lido, pulverulento. Sucintamente la experiencia consistió en diluir el
metol irradiado con el resto de los componentes de la solución reveladora,
sumergir en esta solución filmes blanco y negro expuestos, y revelarlos a
temperatura, agitaci6n y tiempos constantes. Siendo fijados, lavados y
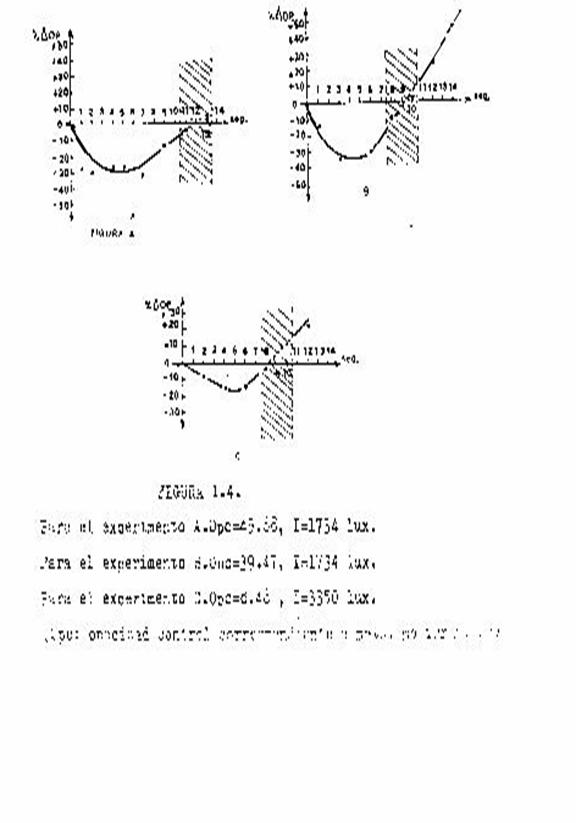
secados los filmes, fueron luego medidos sus valores de densidad óptica (D).Los
primeros resultados de la opacidad (D = log Op) expresados en
funci6n de los tiempos de irradíaci6n del metol fueron
presentados por C. A. Leguizam6n, J. M. Cordero, y A. N. Zaretzky (1984).
(Figura 1.4.)
L
+150 ‑ +40
1.40‑ +30
~30 ‑
.20
+lo
1 2 3 4 5 el ‑1
4.20‑ 7. 11121314
0
1
~
+lo‑
1 2 3 A 5 6 7 8 910 14 o.
o‑ ‑Seo. ‑1
0
‑20 0
30
s0
o
FIGURA 4
'4áOp
t'30
+20
~i 1 12 1314
+ 1
2 3 4 5 6 1 ~e
1
. 1 ~;l~, ~ ~ ' ' ~ . seg.
C
?IGURA
1.4.
Para
el exuerimento A.Ope=45.~8, I=1734 lux.
Para
el experimento B.üDc=39.47, I=1734 lux.
Para
el exDerimen‑to C.Opc=8.4u_‑ , I=3350 lux.
cnrres‑7,~r,,‑,
~nte ~_no


La
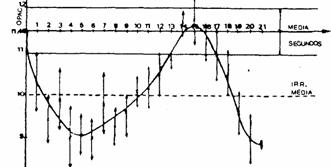
experiencia fue reiterada hasta 21" con Opc= 11,48,I=335ólU'X(Leguizam6n,
C.A,; Cordero, J.M.; y Zaretzky, A.N. 1987a) (Figura 1‑5‑)
Op
15.
14‑
13
12,61
12
1
FIGURA
1‑5
Una
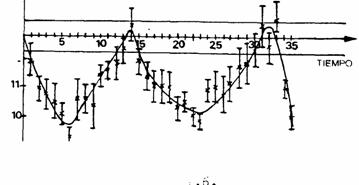
tercera exmeriencia fue realizada hasti 351* con Opc=12,61,I=33501ux
(Leguizam6n, C.A.p Corder, J.1¿‑, ZaretzkY A. 1987b1 (Figura‑‑‑_1.6.).
'
‑8
La
experiencia fue reiterada por G. Peschel y T.Popescu (1988) en el Institut fúr
Physikalische Und Theoretische Chemie, Universidad de Essen, Alemania
Occidental. Los resultados reiteraron el descubrimiento anterior.
El
efecto es llamado Efecto Continuo Peri6dico.
Un
tercer concepto relacional fue inducido por medio de categorías y fue
denominado asignaci6n adicional número uno (Leguizam6n y Zaretzky 1984). Sin
identificaci3n con un concepto conocido, en principio, fue luego identificado
con el tiempo, el que fue interpretado como cumpliendo tres condiciones:
homogeneidad, continuidad e irreversibilidad. Posteriormente la temperatura, la
longitud y otros conceptos fueron reconocidos a través de esta asignaci6n.
La
teoría de reticulados fue introducida en la teoría relacional (Leguizam6n, C.A.
Zaretzky,
A.N.y Viogg, B.M.1983).
Considerando
procesos relacionales de dos átomos, distributivos, fue obtenido un reticulado
L 13 de trece elerientos, el cual es el: elemento fundamental en estos
desarrollos.
Los
átomos en interacci6n fueron identificados con la naturaleza física material
(m) ligada a la energía extrínseca (e) para dar la duDla me, y también Dor m
ligado a una energía extrínseca específica e y a una agier‑ac4‑6n
adicional v rara dar méy. En L 13 ar,‑,recen u‑‑,,;‑Posí‑ciones
del
tipo me v mey, donde la operaci6n "v" significa que las proposiciones
originales operan conjuntamente. Cuando existe interacci6n de me y mey, se
produce la nueva proposici6n me a mey, aonde me y mey identifican las
respectivas Dartes realmente intervinientes.
El
reticulado L 13 pertenece a la variedad ecuacional H 4 de algebras pseudo‑booleanas,
H
4 x v (x ‑> (y v ‑1 y) ) = 1
(x
‑‑‑‑yY) V (y 3.
x) V C (x‑‑‑‑:> y) x)]
me v rriv v rne
arTrey
rne v meemey v
rrCy mZyvmenmEy
rne v m nig~ V MEY
rne mey
V Qy*
m LTY*
3
FIGURA‑ 1‑7
Un
conjunto de importantes subreti‑culados
son
obteníbles a Dartir de L 13‑ Así, se encuentran
L
(algebra booleana) L y L pertenecientes a la va
4 ‑1
5 8 ~
riedad
H L
y L pertenecientesa la variedad cw
49 6 9 ‑5
‑lo
H
2 x v ‑1 ‑1 x=
H
3: x v (x ‑‑‑‑‑XY v ‑1 yY1)=
H
5: x v (x ‑~ (y v n y)
~x
v ‑~‑1 x= 1
6:
(x ‑7 y) v (y x)=
7
x v ‑‑jx= 1 (algebra de Boole)
H
7 C H 5 H
ó C‑ H 2
H
5 C‑ H 4 H
3
1
:meernEy
I=
me*v mly
1
=rne v mUy
v me*v
ni 9 mjy
> éy*
me mly
mes Miyo Me*
L
6
0 4‑ <
0 L5 0
i=lll;syv
me a miy z mevnic‑y
menm~y ¡Tip*v
filly me v m né >v MIy
m_y v'm.y me
mé*v
mie‑y* > MEY
me* mly* <me* >mevo
0 L8 0 L9
FIGURA
1.8.
‑11
Anteriormente
fue dicho cue el objetivo de esta teoría relacional consistía en identificar
los conceptos relacionales y las condiciones bajo las cuales interactúano
Algunas de éstas condiciones podrían ser*ded‑,, cíbles de las
aplicaciones de la teoría y también encontrarse‑ nuevos conceptos
relacionales.
Los
conceptos relacionales son identificados como elementos algebraicos m.,ele, y,
cuyos axiomas deberán ser definidos sobre la base de las condiciones
establecidas por aquellos conceptos. Así, un elemento del reticulado
identificado por mey, aeberá en el futuro corresponder a una operaci6n
algebraica resultante a partir de los axiomas de loá elemento á‑‑algébraico
s ‑ De esta manera, la variedad algebraica final obtenible a partir
del correspondiente reticulado, H 4 si es L 8 0 H 5 si es L,, será dependiente
de las condiciones que cumplan cada uno de los elementos del reticulado.
Cada
uno de estos reticulados da lugar a una respuesta en el elemento universal 1.
El
reticulado L 8 es particullarmiente interesante
Allí,
aparece el elemento me a mey que, como fue dicho,
corresponde
a una nueva proposici6n debida a la interac
ci6n
de me y méy, por la cual la asignaci6n adicional
número
uno y se encuentra involucrada en el proceso.
Si
los comportamienúos relacionales son interpretados ror
L
a y aquellos son dados coiLo funciones de la asiEnaci6n
y,
entonces si ésta es representada en el eje real X
cumpliendo
una tor)olo>~la no Hausdorff, entonces las
funciones continuas del
tiro C (x, tR) no oera
0
1
‑12
k‑arán puntos.
Esto fue obtenido en (Legui
zam6n, C.A. y Allignani, DI.A. 1988) conside
rando
el concepto abstracto de tiempo bajo
las
condiciones de homogeneidad, continuidad
e
irreversibili.dad.
2.
SOBRE EL RETICULADO DE LA FLECH.k HEYTING.
La
obtenci6n del reticulado L 13 de
riv6
en el reconocimiento de una operaci6n
algebraica
denominada flecha Heyting, y defini
ble
as!: x C‑ L, a ^ x ‑' b x
1~‑ a 1 b,
0
sea a b= max x c‑ L: a ^ x
!iz b 1 ‑
La
flecha Heyting dual es definible como a v~.. b= min x é_ L: a v x 7/ b~
Un
álgebra universal <L;‑v,/\,‑;~0,1> es llamada un
álgebra Heyting si, y solo si, <L; VI^ 0,l> es un reticulado
acotado tal que Dará todo a,b e L, el elemento a‑‑9b o£L es el
Dseudo complemento de a relativo a b. (Rasiowa y Sikorski 1963 lla‑man
a esta álzebra como álgebra pseudo‑booleana (PBA».
En
forma similar se define
el ~5lFe
bra
Heyting dual~L,,v,^ 0,1>
.
El
reticulado L 13 es una doble álge~ bra Heyting1 ‑v 1\
\ l3y y y
La
flecha Heyting es ‑,)artic:llla.~‑~i,er‑I~e imnortante entre
elementos no Conrarables (ailb) por cuanto la flecha indícarla una nuev~‑.
oneraci6n entre ei‑ei,,~entcs no oraenanos, de :acuerco.
al
con llantc uarcialmente ordenado IC‑
1
1
‑13
Sea
L una PBA; a e L. El elemento n a <‑2 L es el pseudo complemento de a,
¡.e. xi~~‑Ia áí a ^ x= 0.
Las
siguientes propiedades serán utilizadas en este trabajo:
Sea
L una PBA; a,b <Z‑LL. Entonces:
a
‑‑~ ‑1 ‑1 a
a= a
a
~e b a
7/ b
(a
v b)‑‑ a b
(a
^ b) =_1 a b (Varlet,
1972)
Sea
L una PBA. Entonces B(L)= x C‑_L/X=VI x
,le
elementos cerrados de L. El orden parcial de L
parcialmente
ordena B(L) siendo este áltímo un ál
gebra
Booleana <B(L); U , ^ , ‑1 0, l> para el cual
a
U b= ‑I‑I(a v b) se cumnie.
El
conjunt.o de elementos denso D(L)= ~X e L/‑1 x=( y es un filtro
(Kitrifíak 1974).
Un
filtro es una colección no vacia F de ele
mentos
de L si es verificado:
Fl.
Si fi C‑ F y f t~‑ x x
C‑ F
F2.
ii a,b C‑ F a
^ b e F
f
3. 0
Un
ideal I es defírido en fo‑.‑ma dual (‑‑‑~asiowpy
Sikorski IG.631).
Si
a es un eleniento de L, a ~ 0, entonces F(a) denota la familia de todos los
elementos x de L zai‑ oue a x. Entonces ¡?(a) es el filtr9 zrinciral
asociado
a5,1 a.
‑14
Si
L es una PBA fihit2.,entonces sus filtros son sus filtros principales.
Una
PBA es de orden 3 si ést cumple la identidad x v (x ‑:>(y v1 y)= 1
(Káltriñak 1977).
El Reticulado Flecha Heytin .
En
todo este trabajo trataremos con álgebras pseudo‑booleanas finitas,
Sea
L una PBA.Siguiendo a Birkhoff (1984) si a,b G L entonces a ‑;~ b‑_z
1 =MWLX ~ Q_ L/a í\ x t b
La
Drevia definici6n Duede ser vista a
través
de la siguiente nueva definici6n, en el caso
a b
(a es no comparable con b):
a
‑ b= z 2 ~‑max tx &_L/x C= F(b)j1 F(a)
and a,^x=
=
a,,, . Obviam‑ente z 1 = Z 2
Definici6n
Sea
L una PBA. Sea OC ,=~x 6~ L/ x=a ‑7 b; a, b E. L, a b~u~O~U ll~
El
orden parcial de J F es definido como la restricci6n del orden Darcial de L.
Entonces <~~ F es un Doset.
Si
x i x j y x i v x existen
en £ F
para
todo x i x j £ F entonces F
es el reticula
do
L., llaínado el reticulado flecha Heyting.
L o?
F L LF
T
2.1
‑15
Debe
ser notado que L F no es considerado un subreticulado de L y sus propiedades
deben ser estudiadas independientemente.
Definici6n
Un
nodo n en L es un elemento el cual es comparable con cada elemento de L (Balbes
y Dwinger 1974). Teorema 1
Sea
L una.PEA. Si L tiene nodos n 0,1 tal que ambos F(n i ),e I(n i )tienen
elementos no comparables, entonces los resultados de las Flecha Heyting entre
elementos no comnarables de L es un roset ,P,(pero no un reticulado). Prueba
Id a, b e F (n i a b, z a ‑‑7 b y z j b
‑>a
pertenece
a F(n i V a, I
(n i ),a~ Ii b' z i
b'
5
y
z b 7a'
pertenece a I(n i ».
Debido
a la Dr6xima pronosici6n 1, z líz j
(y
z, z 1 ).
i j
De
acuerdo a la defínici6n delorden parcial
en
4 n i F y entonces 3 Zlyz 21
zl',z2' tal cue
1
1
inf(z1,z 2) y sup(zlyz 2
) no existen a.
Las
siguientes Dronosiciones son triviales:
Sea
L una FBA; a,bc‑ L; al/ b entonces
1.
Si a ‑>b= z entonces z 11 a
2
‑ a b=
z 0
a b=
z j_
‑17
clase
ecuaCional de todos los reticulados relativamente pseudo‑complementados),
el cual es caracterizado por la identidad x v (x ‑‑;~ y) Si y= ~
D(L) x entonces x v‑1 D(L) X=1 ‑Y xC‑D(L);
x '^"
‑) x=z: z = min D(L)
D(L) 0
0
entonces
D (L.) es un álgebra booleanan,
12. Sea
L una PBA de orden 3, z 0 ‑‑minD(L),
ID(L)j > 2,
a
~ D(L), a Y zo 1,
a // Z.. Entonces a‑;>z 0 Z 0
Prueba
Como
a z,‑‑‑>
a v Z ~> z a v z Z
0 0
k
Z
C‑D(L) (por que D(L)=F(z ) y Z ‑:> Z y
z Z
k 0 k 0 k"'
0
como
z k & 1 sea z j =~ D(L)'k* Este z j
existe
porque
L es de orden 3, entonces D(L) es un
álgebra
booleana (prop.11).
Entonces z
j =‑] D(L) z k= 1 D(L) (a v z 0 a v z 0 ‑
;7zo=
::(a z
0 ) ^(z 0 ‑? z 0 )= (a ‑? z 0 1= a ‑>
z 0
Entonc
e s a ‑> zo= Z.; y Z ~‑‑ D (L) z z
la .
J
j j 0
13. Sea
L una PBA con dos áto.,rios a t y a t 2*
z 0 = minD
(L) ; a, b C~ a ~ D (L) b D(L) , a b.
Entonces
a b zo.
Prueba
Sea
a b z Entonces
z,>
0 b.
Pero
z ~¿ 'b ‑jues b
0 D'L.)
‑18
Entonces
z b.
Como
L tiene dos átomos a t_ y a t es
Z.=
a t v a t 2. Si z 0 >b entonces es J. b= a t b=a
t 2.
Supongamos
b=a Como a//b es a;7 a Entonces
t t
2
z
0 A a=at 2 .
Pero
z A a.,‑b Dor ser a b=z
0 0
Luego,
a z ^ a,‑'‑b= a Entonces
t
2 0 t
l
a z
a Absurdo
t 2 t
,
14. Sea
L una PBA. Si L F existe entonces B(L)S L F.o La prueba es inmediata.
15. Sea
L una PBA. Si L es un álgebra booleana, entonces B (L) L F
Prueba Sigue de la proDosici6n 7.
Observaci6n
La
inversa no es cierta. Por ejemplo en L 5 es B(L) ‑L F pero L 5 no
es un álgebra booleana.
<
5
FIGURA
2.2
‑19
Teorema 2
Sea
L una PBA de orden 3, L teniendo s6lo
dos
átomos at 1 y at2, z 0 =minD(L), ID(L)/72 y
V
a ~ D(L), a //z 0 es a v zo~ 1. Entonces, 1 LF~ 2 t
n
‑71 2, n finito.
Prueba
at,
_>a t2 =7atl y at2 at,
at 2
Entonces
‑lat 1 =lla t2 A 0 y ‑la t2 =Matl y hay s6lo dos elementos x:,
y4!~: L tal que x=‑71x e y=11y. Entonces B(L)= 1 OIX9Y11 y
entonces
jB(L)j=
4 (1).
Además,
B(L) C L (prop‑14) (II).
F
Si
x > at, y x > a t2=:>1 x= 0 (prop.6)
entonces
x C‑ D(L) (III)
Además
z 0 ~ L F (prop.9,12,13) (IV)
Si
L es de orden 3 entonces D(L) es un álgebra boo
leana
(prop.11). (V)
Debido
a (I) y (III) es
LIP
G B(L) U D(L) (VI)
Pero
B(L) n D(L)= t 1 (VII)
Debido
a (VI),(IV) y (VII) es
IL
F 1 = 1 B(L) 1 t 1 D(L)( ‑ 2
Debido
a (I) y (Y) es
1 LF~ 4 t ~ D(L) 2 D(L) 2
entonces
1
L~,, 2' ‑,‑ 2, n=2, 3, ....
m (m poroue L es‑ ‑
fini
‑20
Estos
desarrollos algebraicos constituyen un nuevo elemento de análisis te6rico que
ayudaría, entre otras cosas, en la tarea de determinar las caracterIsticas
experimentales de la operaci6n flecha.
De
hecho, el reticulado de la Flecha Heyting constituye un nuevo aporte a la misma
teorla de reticulados.
‑21
LA
INTERACCIOI~ ANTIGENO‑ANTIGU‑‑;RPO
3.1.
Consideraciones biol6gicas del_problema.
El
sistema‑inmunol6gico es el oue reconoce y resDonde a la
invasi6n de sustancias extrafías en el organismo. El sistema comprende células,
denominadas linfocitos y moléculas llamadas inmunoglobulinas.
Las
sustancias extrafias capaces de producir una respuesta se llaman antígenos. Las
porciones de antígeno con las cuales interactúan las inmunoolobulinas se llaman
epitoDes o determinantes.
La
inducci6n de la respuesta es precedida Do el reconocimiento llevado a
cabo por los epitares y la moléculas de inmunoglobulina, las cuales
funcionan com receptores sobre las membranas de los linfocitos. Este
trabajo analiza la primera etapa dada Dor el reconocímiento.
Los
linfocitos se diferencian en células T y células B. Estas áltimas sor. las
precursoras de las células que secretan anticuerros, mientras que las células T
sintetizan nero no secretan gran cantidad dE anticuerpos. Intervienen,
asímismo, como reguladores de la respuesta.
Los
anticuerros son n‑‑o‑lu‑eínas globulínicas formadas por
el entrelaizamiento de una cadena pesada y una liviana de DoliDéD‑tw‑idos.
Existen grandes dí‑ferencias entre las secuencias de los 110 príameros
resiátios, constiti).yena'o la regi6n variable V.
de
esta regi6n hay sli't)secje‑ri,,‑s
.,ue

‑22
tienen
mucha variabilidad, const‑ituyendo la regi6n hipervariable. El plegado de
la cadena pesada y liviana de las regiones hipervariables constituyen el sitio
de combinaci6n del anticuerpo con el epitope antige`nico.
El
resto de los aminoácidos en cada eadena del anticuerpo tienen menos
variabilidad constituyendo la regi6n constante C. Estas regiones determinan
diferentes clases de inmunoglobulinas, siendo las más conocidas la Ig G e Ig M.
La primera de ellas tiene dos sitios de combinaci6n y la segunda, diez.
Un
elemento muy importante, en esta estructura y oue forma parte de ¡a regi6n
constante de la cadena pesada es la bisagra. Esta tiene una cierta
flexibilidad y permite movilídad lateral del sitio de combinaci6n. De acuerdo a
esto la distancia entre sitios Duede ser variable.
Para
que se produzca la respuesta es necesario que haya contacto entre célula B y
antígeno, lo cual, bajo apropiadas circunstancias, disrara la diferenciaci6n y
proliferaci6n celular, y culmina con la proli‑feraci6n ale anticuerros.
Este contact‑o se realiza entre los sitios de ligadura de los
anticuerpos‑receptores cue se encuentran en la‑suDerficie de
las células B y los epitoDes de los antigenos.
‑23
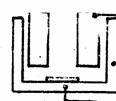
epitOpe antigeno
bi sagra 1^0
Sitio de ligadura
LYr\
r e le l: to r
Superficie celula B
FIGURA 3.1.1
La
ligadura entre sitios de combinaci6n de los receptores y eDitopes ele antígenos
puede ser de varias formas, influyendo sobre la inducci6n de la resDuesta. Si
un epitope se liga con un sitio de combinaci6n se dice que la ligadura es
simple.
FIGUR.A, ^j.1.2 a
j
Si
dos enitopes se liz,ran a dos sitios del mismo recent(r se dice que la ligadura
es intramolecular
‑24
8~'~"7
FIGURA 3.1.2 b
y'si
esto sucede con sitios de dos receptores distintos, ésta es una ligadura
cruzada (De Lisi,
1976;
Roitt, 1978).
FIGURA 3. 1.2 c
Dos
asuectos de importancia en el reco‑nocimiento antigeno‑anticuerpo y
en la inducci6n de la resnuesta posterior serán es‑vecialmente tenidos en
cuenta en este análisis. Uno de ellos es el Darel fundamental que cum‑ole
el
‑25
ligado
cruzado en esta inducci6n. Según Becker y colaboradores (1973) hay evidencias
que el ligado cruzado es suficiente en algunos sistemas para disDarar la
activación y que, aún con s6lo dos receptores involucrados (es decir, con un
solo ligado cruzado) ésto Podría llegar a suceder. Esto Darecerla justificarse
en el hecho que el antígeno ligado cruzado es considerablemente más estable que
uno ligado simple. Entonces, un. ligado cruzado podría mantener una célula el
tiemDo su‑ficiente para que una dada señal mitogenética no especifica sea
liberada (Coutinho y MUller, 1974). 0 sea, que el ligado cruzado sería el
mediador Dara la liberación de la señal. Como consecuencia de ésto se'
le dará especial valor a uno de los factores más importantes que
favorecen al ligado cruzado, este es la flexibilidad de la bisagra.
La
distancia entre sitios de ligadura de los receDtores guarda un rol fundamental
en relación a uno de los conceptos relacionales (asignaci6n adicional número
uno:y) y a la misma resuuesta obtenida del proceso en relación al álgebra
resultante. El concepto de distancia concierne, como se dijo, a la distancia
entre sitios de ligadura de los recentores. La variaci6n de dicha distar‑cia
será concerniente a la flexibilidad de la bisagra y a la roblaci6n de células
3, las rue variando sus dimensiones y la concentración ae recezt‑ores en
ellas varían también la distancia entre sitios.
‑26
3.2.El Modelo Relacional
Teniendo
en cuenta las consideraciones
anteriores
la representaci6n relacional es inme
diata:
1. Existen
dos naturalezas físicas materiales m 1 (sitios de recentores) y m 2 (eDitopes).
2. A
m 1 le corresponde una cantidad de sitios de receDtores presentes en la
superficie de las células B que se encuentran en un determinado medio. Existe
una energía' extrínseca ¡dentificada con "é 1 y donde y concierne al
concepto de longitud int erpretado en términos de una variaci6n continua,
homogénea e irreversible. La energía esDecífica e 1 se interpreta como
inherente a la disDosici6n de los sitios y entonces concierne a energía/unidad
de longitud. Se define así la proDosici6n mi _¿ ly1(Dara yyrepresentando una
distancia dada).
3.
A m le corresponde una cantidad de eDitopes 2 en relaci6n a la cantidad de m 1
para el medio en el que se encuentran.
4.
Bases te6ricas (Lep ‑‑‑ninan
zuizam6n
1975a) deter` que toda nacuraleza física material, en este caso m2, tiene
energía extrínseca natu‑ralmen
te
liada: e*. Así se tiene la proposición
2
m
e*
2
2*
5.
r;l reconocimien‑,o del proceso de inzeracción
entre
los
~..to.~ios
m e,y y ,‑" e es Drsc‑ic,‑
ro
1
~ 2 2
nor
esi cruzada‑ entre eDito‑Jes
y si
‑27
tios de recertores y
expresado por m 1 e 1 y a m 2 e 2 (ig
6. La
teorla relacional expresa que la interacci6n de dos átomos produciendo una
nueva proposici6n (ni) da lugar a lo que es denominado un argumento relacional
de tres ramas
m
e. m
gy*,
2
2
3.2.1
7. Sobre
la base de! argumento anterior y del sígnificado natural de los conceptos
relacionales m 1 e 1 1 y Leguizam6 y Zaretzky en (1989) han determinado que en
térm.inos de retictilados se obtiene el reticulado L 13 (figura 1.7)
relativamente Dseudo‑complementado.
8.
De acuerdo a las consideraciones de los puntos anterior el proceso de
reconocimiento antígeno‑anticuerDo es ¡de tificado por el subreticulado L
a de L 13 (figura 3.2.2). el
‑ryley
V a
m
2~e2*
V M11,y
&e OM8y
r"2
m
mj
2 y*
0
1
‑28
El
elemento 1= mj1y V IR reDresenta todas las ligaduras cruzadas DOsibles.
Leguizam6n
y Allignani (1988) han estudiado la resDuesta a este proceso algebraico para
deterulinadas condiciones de la variable tiempo. Sobre la base de continuidad,
irreversibilidad y homogeneidad para el tiempo representado sobre la recta real
X,existen pos'ibles intervalos que definen una topología sobre la recta.
Segán
De Lis¡ (1980) es posible estimar un rango de distancias entre receDtores de
una célula B en funci6n de su radio y de la concentraci6n de receptores en su
superficie. Teniendo en cuenta las consideraciones de homogeneidad, continuidad
e irreversibilidad para las distancia, se definen los intervalos de la forma
(0,a] los que determinan la subbase para una topología G no‑Hausdorff
sobre la recta real positiva X. El dato a refiere a la distancia máxima
entre sitios en cada célula.
Las
condiciones establecidas sobre la energe
Ía
extrínseca determinan la posibilidad de una variaci6n continua de la másma
cuando se encuentra ligada a la naturaleza física material. Esto corresT)onde q
e 1 y cuando integra la nrorosici6n r. 1 z 1 y a m 2 e 29 con y variando en
princirio, en forma continua Y homogénea.
‑29~
Dado
lo anterior, para y representada sobre la recta real X con topología no
Hausdorff, entonces las respuestas obtenibles mediante el arreglo algebraico
(X,5R)
de fun
de
L 8 son identificadas por la clase C 0 ciones continuas que no separan puntos
(Leguizam6n y Allignani 1988).
Surge naturalmente úl análisis oue y, la distancia, está
involucrada en el proceso.
La
clase e'(X,íR) conti‑ene funciones de distin
0
tas
formas que toman máximos Y/o mínimos en el rango de
todas
las distancias posibles. Existiendo uno o más da
tos
para los cuales la cantidad C de ligaduras cruzadas
es
un máximo, entonces sería apropiado encontrar los va
lores
d
0
Para
una distribuci6n normal de células B en
funci6n
de sus radios, entonces es conjeturable obtener
una
curva del tipo de la figura 3.2.3.
C^
a
Min do
bmax
‑7
i G'T2 3.2‑3

~30
El
reticulado L. pertenece a la variedad ecuaCional H 49 Dor la cual entonces
el Droceso de ligadura cruzada tiene luga .
El
estudio que sigue concierne a la aDlicaci6n de los desarrollos sobre el
reticulado de la Flecha Heyting L F (punto 2). En Leguizam6n (198d) fue
definido el reticulado Flecha Heyting Dual DL F tal que la flecha dual se
define: a ‑&~b= min x C= L/ a v' x > b
El
problema de la interacci6n antígeno‑anticuermo Duede ser interpretado en
términos de sendos reticulados L F(8) y DL F(8) Dor cuando el reticulado L8 se
encuentra dentro de la doble álgebra Heyting
L
8; A . v, p ' '
o, i >
La
arlicaci6n de la operaci6n Flecha Heyting entre elementos x (E L no
corDarables, deterinina,por el Teorema 2,el reticulado. de la figura
<.2.4.a,y el de lía Flecha Heyting dual (Leguizam6n 1988) según aDarece en
la figura 3.2.4.'b.
?y
m e,y
m
e'\,/ *me me*
22 1
1y 22 m 11 1 y
0
L DL
F(8)

‑31
Naturalmente,
por las definiciones de las operaciones dadas por sendas flechas, los elementos
obtenidos en L F(8) corresponden a resultados dados ror incrementos de energía,
y en DL F(8) por decrecimientos de energía. Ambos,LF(8) y DLF(8)eH5
El
análisis biol6gico radica entonces en descubrir en la estructura algebraica
original L 8 cuáles serían las oper~~.ciones Dosibles, definibles por un viable
‑proceso algebraico, oue conllevasen a una disminuci6n o eliminaci6n de
las ligaduras cruzadas, representadas Dor la proDosici6n a . Esto se
logra Dor ma segunda obtenci6n del reticulado Flecha Heyting Dual DL(DL F(8). )
como se ve en la figura3.2.5.
m
1 e 1y ffl1y
0
DUDL
F(8»
FIGITRA 3.2.5
El
reticulado anterior significa Que la pérdida de energía en el sistema a través
de la oDeraci6n Flecha Heyting Dual entre elementos no c=parables, disminuiría
el nImero de ligaduras
‑32
cruzadas.
Obsérvese que el álgebra resultante de
DL(DL es
no modular.
Esta
aplicaci6n muestra c6mo el razonamiento y las herramientas provistas Dor la
Biologla Relacional permiten analizaxun proceso, inf erír el comportamiento
algebraico que el‑ sis‑tema deberá tener, dar pautas sobre la
influencia que una determinada variable (en este caso la distancia entre
sitios) puede tener sobre la producci6n de la interacci6n buscadae inducir a la
búsqueda experimental de la Flecha Heyting Dual ya que su producci6n entre
elementos no comDarables afecta la concreci6n de la interacci6na.
‑33
4.El Efecto Continuo Periódico sobre un Nutriente de
Plántulas de trigo
Según
fue establecido te6ricamente el Efecto Continuo Peri6dico es un efecto general
sobre la materia. La verificaci6n de esto m obtuvo experimentalmente
irradiiuido con bajas energias para‑metil aminofenol sulfato y midiendo
los resultados de la opacidad en filmes. En este trabajo se utiliza otra
sustancia, el nitrato de potasio, el cual es utilizado como nutriente de
plántulas de trigo, midiendo elefecto sobre éstas.
4.1.
DisDositivo de irradiaci6n.
El
aDarato de irradiaci6n consiste en una lámpari de mercurio General Electric H
100 Watts A 4 T. El obturadc es a diafragma, Kodak, ubicado inmediatamente
arriba de un filtro de interferencia marca Ealing >,=54Ó,l nm, ¿X = 8 ‑rim,
0 = 25,4 nm. El filtro se asienta sobre un colimador de aluminio opaco, con un
diámetro adecuado tal que el haz de luz determina una secci6n de diámetro igual
a 20 mm en el fondo del vaso opaco que contiene la sustancia a irradiar.
El
haz se obtuvo uniforme, sin anillos ni seccio.z. de mayor iluminací6n, lo cual
fue verificado ímediante un fot6metro J‑16 Tektronix. La cáinara de
irradiaci6n fue mantenida con ambiente seco. La sustancia irradiada, nitrato de
Dotasio en Dolvo seco, fue dejada desde 24 horas antes de la irradiaci3n en
desecador. La altura de la
lánpara
fue ajastada de manera tal que la iluminarcia
‑34
sobre
la muestra fue de 3140 lux + 10 lux (lumen/m 2 ) durante la
irradiaci6n.
Se
irradiaron muestras de 20mg de nitrato de potasio por semilla durante tiempos
entre 14 y 35 segundos (± 0.05seg.), segundo a segundo.
I‑LAMPARA
'^OBTURADOR
FILTRO
77
COLMDOR
‑
Li VASO
SUSTANCIA
A IRRADIAR
FIGU.RA
4.1.1
4‑
2. Siembra
Se
seleccionaron 288 semillas de trigo Inta Pampa, todas de similar Deso (50mg
aproximadamente) y tamaflo, con contextura homogénea y excluyendo aquellas que
presentaban anormalidades.
La
su‑perficíe de las semillas fue esterilizada sumergiéndolas durante 45
minutos en una soluci6n al l1,', de hiDoclorito de sodio.
El
lugar Dara la germinaci6n fue preparado con cantidades homogéneas de
arena lavada y esterilizad`a por calcinación. ¿Se acondicion6 el ambiente
impidiendo la entrada direcia de luz solar, registrando valores de iluminaci6n
similares sobre toda la sizi,DertL'icJ. e se7,2rada. (Ic‑~ 50 lux). La
tera
‑35
peratura
fue la del ambiente, manteniéndose entre 16ºC y 282C. Las semillas fueron
ubicadas distantes entre sí 5 cm, y dispu?stás en hileras db 12 semillas.
Se
utilizaron 24 semillas para control (C) y 12 Dara cada uno de los
distintos tiempos de irradiaci6t La disposici6n de las hileras fue obtenida
mediante una tabla de números al azar. La profundidad de siembra fue de Q.5,
el~~
4.3.
Proceso experimental
A
cada recipiente (opaco a la luz) conteniend( 20 mg de nitrato de Dotasio fueron
agregados 36m1 de agi bidestilada, agitando la disoluci6n durante 15 minutos.
Exactairente a los 15 minutos de la disoluci6n fueron incorporadas 12 semillas
a cada recipiente. Después de 105 minutos las semillas fueron retiradas de la
disoluci6n e inmediatamente sémbradaw. Simultáneamente, similar secuencia fue
seguida con nitrato de potasio no irrz diado utilizado como control (C), con
peso y volúmenes corresDondientes a 24 semillas.
Luego
de la siembra,a:cada‑‑sem'illa‑'ae le‑‑agre ron
2mi‑de agua bidestilada, repitiendo esta operaci6n día mor medio.
A
los dos días de la siembra se observ6 la aparici6n de los primeros brotes.
La
experiencia se dio por finalizada 23 días desnués del día de sierabra
obteniéndose un porcentaje de germinaci3n que en ningún caso fue inferior a
83.33
Las
plántulas, después de extraídas de la are fueron lavadas y secadas,
manteniéndoselas en estufa 5452C durante 3 horas. Las raíces fueron
pesadas(±O,OOC
‑36
4.
4. Análisis de los datos
Fue
obtenido el Deso de las raíces.
Los
resultados correspondientes a
las
medias y desviaciones del peso (Desvío
Standard
4 ;E (X i‑ j)2/n_, »aparecen en la tabla
1
y el gráfico correspondiente en la figura 4.4.l.,
Tiem‑no Kedia Desvío
|
Control C
|
0.034
|
0.007
|
|
l4"
|
0.012
|
0.002
|
|
15#1
|
0.019
|
0.005
|
|
16,1
|
0.018
|
0.006
|
|
l7"
|
0.024
|
0.005
|
|
18,4
|
0.019-
|
0.004
|
|
1911
|
0.034
|
0.004
|
|
20"
|
0.031
|
0.007
|
|
21"
|
Q-031
|
0.006
|
|
22"
|
0.036
|
0.005
|
|
23"
|
0.033
|
0-005
|
|
24»
|
0.037
|
0.006
|
|
251*
|
0.027
|
0.008
|
|
26"
|
0.032
|
0.005
|
|
27n
|
0-041
|
0.009
|
|
280
|
0.048
|
0.005
|
|
29"
|
0.029
|
0.007
|
|
3011
|
0.019
|
0.007
|
|
3111
|
0.017
|
0.006
|
|
32"
|
0.011
|
0.003
|
|
330%
|
0.009
|
0-003
|
|
34"
|
0.010
|
0.003
|
|
1 351*
|
0.020
|
1 0.006
|
TABLA
1
‑37
Desvío Standard
0.050‑‑~
1
0.0401
C=
0.0341 T T k‑f 1 Y ‑7
T T L 1
‑‑,II
0.020~
0.010
Oi
14 16 18 20 22 24 26 28 30 3
2 34 36 ser
FIGURA
4~4.1
Los
puntos experimentales muestran sus desvíos standard. Un análisis de Fourier
permití6 obtener puntos Dor los cuales pasa la curva de ajuste.
Para
comDarar las muestras control contra cada una de las medias de los otros
tratamientos se utiliz6 el test estadístico de Dunnett (Steel y Torrie, 1960).
Se
consider6 un nivel de significaci6n de p=0.99. De acuerdo con ésto el análisis
muestra diferencias significativas entre las muestras control y las
corresnondientes a 1411,15",1611,17",180,2811,30'*,31",32'9,
33",_‑WI y 35".
‑38
4.5.
Los resultados
La
curva dada por los pesos de las raíces obtenida en funci6n de los
tiemnos de irradiaci6n sobre el nitrato de potasio, presenta similares
caracterIsticas a la opacidad en filmes cuando se revelaron en D‑metil
aminofenol sulfato diferentemente irradiado (Leguizam6n, Cordero y Zaretz.ky
1987). Más aún, el período 6DtiMO Dara la curva de ajuste por el método de
Fourier result6 ser el mismo en ambos casos.
Adicionalmente,
se obtuvieron notables diferencias entre los pesos de las raíces tratadas con
nitrato irradiado y las correspondientes al control, tanto de incrementos como
de disminuci6n de ellos, mientras oue otros se mantuvieron en la franja del
control de acuerdo a lo anticiDado te6ricamente y a lo verificado
exDerimentalmente en filmes.
Esta
nueva verificaci6n mediante otra sustancia y otra metodologla, pone entonces de
manifiesto la concreta existencia del E‑fecto Continuo Peri6dico y
claramente muestra su generalidad.
‑39
5.
CONCLUSIONES
La teorla algebraica para
procesos relacionales se ha ido concretando con desarrollos en categorias,
reticulados, topologia y a través de aplicaciones concretas. Este trabajo
aporta un nuevo avance sobre lo anterior por cuanto se exDresan los siguientes
tres concretos hallazgos:
‑ La
definici6n de los reticulados Flecha Heyting y
Flecha Heyting Pual, con
desarrollos de interés matenático.
‑ La
aDlicaci6n de la teorla al Droceso de interacci6i antigeno‑anticuerpo, lo
cual determin6 un reticulad( de ocho elementos perteneciente a la variedad
ecuacional H 4 de álgebras pseudo‑booleanas.
‑ Se ha
verificado nuevamente la existencia del Efectz Continuo Peri6dico con
experiencias irradiando un nutriente, nitrato de potasio, el cual se utiliz6
con plántulas de trigo.
El trabajo también
muestra c6mo los desarrollos matemáticos con los reticulados L F y DL F sor.
utilizados para obtener conclusiones sobre el caso especl~‑'~ico cuando
la rresencia de antIgenos y anticuernos no produce las ligaduras cruzadas que
da lugar al disparo ‑de la reacci6n inmunol6gica. Debe valorarse el
:.'lgebra ror primera
vez obtenida (proceso pseudo‑booli no) en la reacción antigeno‑anticuerpo,
as,.' como desd( ella valorar su cambio (proceso no‑modular) cuando la:
ligaduras crazadas no se producen.
‑40
Debe
ligarse el punto anterior con los resultados reiterados cuando se obtiene la
producción del Efecto Continuo Peri6dico.
Ambos
procesos resDonden a una estructura algebraica similarmente definida Dor un
reticulado L,, lo cual confiere mayor certeza sobre la conjetura que permite
obtener
la
figura 3.2.3.
Se
agradece al Ing. César Troncoso el aporte en equipos electr6nicos y su
mantenimiento mediante los cuales se pudieron eLectuar las irradiaciones.
Este
trabajo fue hecho posible medi‑ante la ayuda econ6mica aDortada ror j.E.
Cordero, M.C. Leguizam6n y A.N. Zaretzky.
‑41
BIBLIOGRAFIA
‑Arbib,M.(1966).Bull.
Math. Biophys. 28: 511‑517.
‑Baianu,I.U970).Bull.Math.
Biophys. 32: 539‑561.
‑Baianu,I.(1971).Bull.
Math. Biophys. 33: 339‑354
‑Baianu,I.(1980).Bull.
Math. Biol.. 42:431‑446..
‑Baianu,I. y
Marinescu,M.(1968).Bull. Math. Biophys. 30:625 ‑Baianu,I. y Seripeariu,D.(1973).Bull.Tilath.
Biol. 35:475‑48 ‑Balbes,R. y
Dwinger,P.(1974)."Distributive Lattices".Unive of lúissouri Press.
‑Becker,K.;Ishizaka,T;Metzger,H.;Ishizaka,K.
y Grimley,P.(I J. Exp,Med.,138:394,
‑Birkhoff,G.U984)."Lattice
Theory".A.M.S..Colloa. Pub.,Vol. ‑Comorosan,S y
Baianu,I.(1969).Bull. blath. Biophys.31:59‑T ‑Coutinho,A. y
Kbller,G.(1974).Scand. J. Immun. 3,133.
‑De
Lisi,C.(1976).Lecture Notes in Biomath.,Vol.8,Springer‑De
Lisi,C.(1980).Math. Biosc. 52:3/4,159‑184.
‑Demetrius,L.(1966).Bull.
Math. Biophys. 28:153‑160.
‑Foster,B.(1966).Bull.
Math. Biophys.
28:371‑374.
‑Katrinák,T.(1974).Bull. de la
Société Royale des Sciences LAge, 43 e année,Nº5‑6,283‑290.
‑Katrinák,T.U977).Algebra
Universalis 7/2,265‑271.
‑Leguizam6n,C.A.(1975
a).Bull. lí.,ath. Biol. 37:565‑572.
‑Leguizam6n,C.A.(1975
b).Bull. 1,lath. Biol. 37:Ó75‑689.
‑Leguizam3n,C.A.(1976).Bull.
Math. Biol. 38:547‑563.
‑Leguizam6n,C.A.(1977
a).Bull. Math. Biol. 30:307‑406
‑Leguizam3n,C.A.(1977
b).Bull. ,i.at.h. Biol. 39:407‑413.
‑Leguizam,3n,C.A.(1982).,~nales
de la Acaáeria Nacional de Exactas,Físicas y Naturales,34:363‑408.
‑Leguizam6n,C.A.(lgbb)."i.owards
an Algebraic Theory for H,
tional
Processesll.i,*.asson,Pari‑s (en orensa).
y
de
‑''a7~emática 2:726‑751
,os~
o L~‑,'~noaner‑‑.c..‑.no de
‑42
Leguizam6n,C.A.
y Zaretzky,A.N.(1984).Revue de Bio‑Mathématique
87:1‑25. Leguizam6n,C.A.;Cordero,J.DI.;Rodriguez,N.R.
y Zaretzky,A.N. (1984).Actas del Segundo Congreso Internacional de
Bíomatemática 1:106~‑124. Leguizam6n,C.A.;Cordero,J.Dl. y Zaretzky,A.N.
(1987 a). J. of Inf. and Ded. Biol. (En prensa). Leguizamdn,C.A.;Cordero,J.ril.
y Zaretzky,A.N. (1987 b). J. of Physiol. Chem. and Phys. 19(1):15‑21.
Leguizam6n,C.A. y Allignani,M.A.(1988).Bio‑Math. 101:31‑45Leguizam3n,C.A.
y Zaretzky',A.N.(1989). Bio‑Math.(En prensa).,
‑Peschel,G.
y Popescu,T (1988).J. Physiol..Chem. and Physics. En prensa.
Rashevsky,N.(1954).Bull. Math. Biol. 16:'317‑348Rashevsky,N.(1972)."Organismie
Sets'1.Grosse Pointe Park, Michígan:J.M. Richards Lab.
‑Rasiowa,H.
y Sikorski,R.(1963).11The Mathematics of Metamathematics".Polska Akademia
Nauk‑Warszawa, Poland. Roitt,I.(1978)."Inmunologla
Esencial".Editorial J.I.M.S.
‑Rosen,R.(1958
a).Bull.Math.Biophys. 20: 245‑260.
‑Rosen,R.(1958
b).Bull.Math.Biophys. 20:317‑342. Rosen,R.(1972)."Foundations
of Mathematical Biology'1.Vol.II. N.York: Academic Press.
‑Steel,R.
y Torrie,J.(1960)..liFrinciples and Procedures of Statistics".New
York.MeGraw Hill. Varlet,J.(1972).Algebra Universalis 2/2:218‑223Woodger,H.U937).I*The
Axiomatic Method in Biology".Cambridge: Cambridge University Press.
1
1
1
1
1
4
.
I‑DI.
ziapoíxtlo
:ba
~ ‑
i
0
1
1
t, ‑
‑zt!:Posi«rivo
32
i
4
‑
i
~5
1
F
Q 2
1
l
1
pe‑
PCIN«
FILM
Aso
AOGA
W‑71A
1.
, , , , , , , , , ', 7‑‑ ‑ , , ‑ L
1
7,7
=Z‑12‑7
AGUA
A 200e
Fi
3
4


TABLE
1
SAMPLE MEAN
VALUE STANDARD DEVIATIUN
c 11,48 0
' 52
111 10.29 0,65
2fi 9,41 0,56
3" 9,87 0,69
4" 9,03 0,69
se§ 9.06 Q47
el§ 8,97 0,49
711 9,79 Q73
811 9,27 0,40
90 9,56 0,54
lo¡¡ 10,00 0,32
ii0 lQ14 0,49
12" .10.46 0.44
1311 iQ
so ql7
14
If 11 * 64 0,29
isit 11
be 0,54
1611 11,17 0,42
170 10,87 0,58
18
te 10,46 0,52
19
lo 9,54 0,48
2011 9,01 Q53
20 8,90
12
CONTROL 1234567891011
1219 131.7 1819 20 2,1
MEAN
IlM
SECONDS
IHH.
lo ‑ ‑ ‑ ‑
‑ ‑ ‑ ‑ ‑ ‑ ‑
‑ ‑ ‑ ‑ ‑ ‑
MEAN
3
TABLE
1
r:
‑t ~,
. ‑1
IALAN
NIALUE STANDARO DEVIATION
(;ONTROL 12,01 0.411
1
4ffic. 11,90 0,45
2
11 10.99 0,34
3
14 10.70 Q41
4
ís 10.31 0,43
5
la 10 0.32
a X32 0,25
7 10.66 offi4
a 10,53 0,37
5 10.24 01»
10 11.32 0,31
11 11,62 0.31
1214 11,72 0,»
13
lé 12,32 0,24
1414 12AS 0,42
15#1 12,04 0.35
id*, 11.44 0,37
1714 1091 0.44
10.81 0,53
10,84 0,47
10.13 0.39.
21 IQ33 0,25
2
2 9.71 Q31
23 151 0.25
24 10.42 Q28
25 lQ54 a46
26 10,21 0.48
27 10.70 0,46
28 11.70 0.51
29 11.77 0.58
30 12,21 Q44
31 12.9 0.61
32 12,42 o~41
33 13.17 Q45
34 10.92 an
» 939 ‑
1
11‑,~,,~,»‑ ‑
.1
~ ‑‑‑~1
opil
13 ‑
1 4t
ig to o « 01 1# ir £í. A~, a t9 ',.1y
34 3,V«3r» time
FIGURE
3
4
i
1
tl,~
o
\ , t~~i
tret
hoy VI* 31
L‑H44‑‑ ‑1
A
‑09.
CIL
‑
amo
q#
ok
~ i

off»
‑ TT
i
i
i .


![]()
![]() Ps Pc Pm
Ps Pc Pm![]() J
J X 1 X2
X 1 X2 
![]() ? Ex 1 } E1
2
? Ex 1 } E1
2![]() J
J






