Práctica Computacional:
La Ecuación de Schrödinger
La figura 1 representa una ``caja de potencial" unidimensional
(1-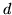 potential box).
Resolver la Ecuación de Schrödinger y obtener el espectro de
energías posibles del sistema.
potential box).
Resolver la Ecuación de Schrödinger y obtener el espectro de
energías posibles del sistema.
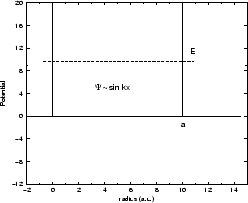
Figure 1:
Caja de potencial unidimensional, de ancho 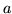 .
.
 |
Procedimiento de solucion: separar el problema en distintos sectores,
solucionarlos independientemente y hacer coincidir las funciones (y sus
derivadas) en los bordes. Finalmente, normalizar las funciones.
- Qué particularidad tiene el espectro de energías?
- Cuál es la mínima energía que puede tener una partícula
(no es 0? por qué?)
- Calcular
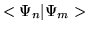
- Calcular
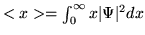 para los 4 primeros
estados.
para los 4 primeros
estados.
- El estado básico de una partícula en una caja (1-
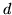 ) es 4.4 eV.
Cómo cambian las soluciones:
) es 4.4 eV.
Cómo cambian las soluciones:
- si el ancho de la caja se duplica?
- si el potencial dentro de la caja es una constante
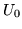 en lugar de cero?
en lugar de cero?
- Un electron en el estado básico está atrapado en una región
(1-
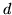 ) de 1 Å:
) de 1 Å:
- Cuánta energía hay que darle para excitarlo
al primer estado?
- Cuál es la probabilidad de que el electrón esté entre
0.09 Å y 0.11 Å?
- Cuál es la probabilidad de que el electrón esté entre
0 Å y 0.25 Å para el primer estado excitado?
- En forma intuitiva, cómo serán estas probabilidades
en los siguientes estados?
Tienden a algún límite?
Por qué?
- Extender el problema general a una caja de 3 dimensiones (3-
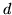 ).
).
- Qué particularidad tienen las funciones ondas?
- Qué particularidad tiene el espectro de energías
cuando se trata de un cubo?
El ejemplo (Notebook)
SCHRO.NB
puede ser utilizado en el programa
MATHEMATICA, para resolver los siguientes ejercicios:
- Hacer un gráfico con las tres primeras funciones de onda.
- Comprobar numéricamente si las funciones son ortonormales.
- Hacer un gráfico con las densidades de probabilidad.
- Verificar los resultados de las probabilidades obtenidas en
la pregunta (I-B-6).
- Hacer un gráfico con la probabilidad de encontrar una partícula
entre 0 y
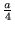 , en función del índice de la función de onda.
, en función del índice de la función de onda.
(*--- Calculo de las funciones de onda en el pozo ---*)
phi[x_,n_Integer,a_] := If[0<x<a,Sqrt[2/a]*Sin[(n*Pi*x)/a],0];
Plot[ {phi[x,1,2],phi[x,2,2],phi[x,3,2]},{x,-1/2,5/2}];
![[Graphics:Images/Schro_gr_1.gif]](Images/Schro_gr_1.gif)
![[Graphics:Images/Schro_gr_2.gif]](Images/Schro_gr_2.gif)
![[Graphics:Images/Schro_gr_3.gif]](Images/Schro_gr_3.gif)
![[Graphics:Images/Schro_gr_4.gif]](Images/Schro_gr_4.gif)
![[Graphics:Images/Schro_gr_5.gif]](Images/Schro_gr_5.gif)
![[Graphics:Images/Schro_gr_6.gif]](Images/Schro_gr_6.gif)
![[Graphics:Images/Schro_gr_7.gif]](Images/Schro_gr_7.gif)
![[Graphics:Images/Schro_gr_8.gif]](Images/Schro_gr_8.gif)
![[Graphics:Images/Schro_gr_9.gif]](Images/Schro_gr_9.gif)
![[Graphics:Images/Schro_gr_10.gif]](Images/Schro_gr_10.gif)
![[Graphics:Images/Schro_gr_11.gif]](Images/Schro_gr_11.gif)
![[Graphics:Images/Schro_gr_12.gif]](Images/Schro_gr_12.gif)
![[Graphics:Images/Schro_gr_13.gif]](Images/Schro_gr_13.gif)
Darío Mitnik
U.B.A.

![[Graphics:Images/Schro_gr_1.gif]](Images/Schro_gr_1.gif)
![[Graphics:Images/Schro_gr_2.gif]](Images/Schro_gr_2.gif)
![[Graphics:Images/Schro_gr_5.gif]](Images/Schro_gr_5.gif)
![[Graphics:Images/Schro_gr_6.gif]](Images/Schro_gr_6.gif)
![[Graphics:Images/Schro_gr_7.gif]](Images/Schro_gr_7.gif)
![[Graphics:Images/Schro_gr_9.gif]](Images/Schro_gr_9.gif)
![[Graphics:Images/Schro_gr_10.gif]](Images/Schro_gr_10.gif)
![[Graphics:Images/Schro_gr_12.gif]](Images/Schro_gr_12.gif)
![[Graphics:Images/Schro_gr_13.gif]](Images/Schro_gr_13.gif)