Práctica Computacional:
La Ecuación de Schrödinger - Estados del Contínuo
Calcular el coeficiente de transmisión 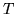 para el problema de
un pozo de potencial de altura
para el problema de
un pozo de potencial de altura 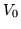 situado entre
situado entre 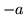 y
y 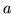 .
.
Al igual que en el caso anterior, se deben separar las distintas regiones,
en las cuales la funcion de onda tiene componentes ondulatorias que
(al construir la funcion total) se desplazan hacia la derecha e izquierda
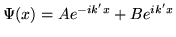
donde
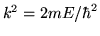 y
y
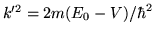
Conviene tambien adimensionar el potencial definiendo el potential strength:
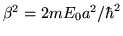
y el parametro
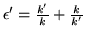
Preguntas
- Calcular el coeficiente de transmisión
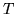 en función de la
energía incidente
en función de la
energía incidente 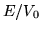 . (Ejemplo: Figura 1).
. (Ejemplo: Figura 1).
- Cómo tiende el coeficiente
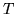 cuando la energía
cuando la energía
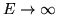 ?
Cómo tiende el coeficiente
?
Cómo tiende el coeficiente 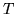 cuando la energía
cuando la energía
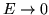 ?
Contradicen estos resultados a los resultados clásicos?
?
Contradicen estos resultados a los resultados clásicos?
- Explicar por qué se producen picos pronunciados en
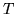 (resonancias), teniendo en cuenta
(resonancias), teniendo en cuenta
- la distancia que recorre una partícula en un recorrido
ida y vuelta adentro del pozo
- la longitud de onda de de Broglie de esta partícula
- Graficar
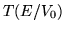 y marcar en el gráfico las energías de los
estados ligados (cambiarles el signo, así aparecen como energías
positivas).
y marcar en el gráfico las energías de los
estados ligados (cambiarles el signo, así aparecen como energías
positivas).
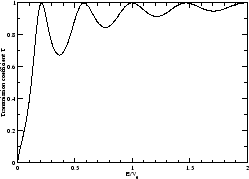
Figure 1:
Efecto Ramsauer-Townsend. Coeficiente de transmisión 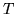 versus
versus 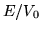 , para un pozo de potencial cuyo
, para un pozo de potencial cuyo 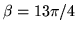 .
.
 |
Parte computacional
Método de diferencias finitas (método de Numerov)
Utilizaremos el método de Numerov, que empleamos anteriormente
para encontrar una solución numérica del problema de una onda (ligada)
en un pozo de potencial unidimensional, limitado en 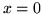 por una pared de
potencial infinito. Ahora lo emplearemos para hallar soluciones en el
contínuo.
por una pared de
potencial infinito. Ahora lo emplearemos para hallar soluciones en el
contínuo.
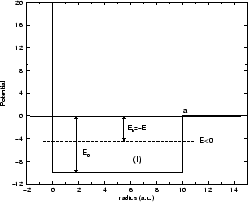
Figure 2:
Pozo de potencial rectangular, de ancho 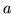 y limitado en
y limitado en 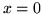 por una pared de potencial (
por una pared de potencial (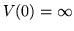 ).
).
 |
- Modificar el programa usado para hallar los estados ligados,
de manera de poder utilizarlo para
energías positivas.
- Graficar la función de onda resultante, junto con la
solución ``libre" (en la cual el potencial es
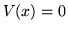 ).
A partir de un cierto valor de
).
A partir de un cierto valor de 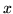 , se verificará que las
dos ondas son iguales, excepto un corrimiento de fase
, se verificará que las
dos ondas son iguales, excepto un corrimiento de fase 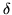 .
Calcular el corrimiento de fase para distintas energías.
.
Calcular el corrimiento de fase para distintas energías.
- Difícil:
Verificar si cambia la amplitud de la onda en la zona del
pozo, y si esta tiene alguna relación con el corrimiento de fase.
- Sólo para avanzados:
Añadir al pozo un potencial centrífugo
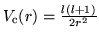 (ver Figura 3)
y analizar las resonancias para el caso
(ver Figura 3)
y analizar las resonancias para el caso 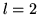 .
Este potencial representa el potencial efectivo para un pozo esférico.
Con los parámetros dados en la Figura, buscar las resonancias alrededor
de
.
Este potencial representa el potencial efectivo para un pozo esférico.
Con los parámetros dados en la Figura, buscar las resonancias alrededor
de 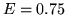 a.u..
a.u..
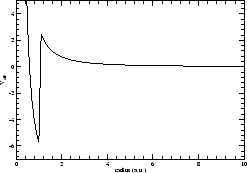
Figure 3:
Potencial efectivo para un pozo esférico.
Los parámetros utilizados son 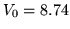 a.u.,
a.u., 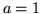 a.u. y
a.u. y 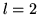 .
.
 |
Darío Mitnik
U.B.A.
![]() para el problema de
un pozo de potencial de altura
para el problema de
un pozo de potencial de altura ![]() situado entre
situado entre ![]() y
y ![]() .
.

![]() por una pared de
potencial infinito. Ahora lo emplearemos para hallar soluciones en el
contínuo.
por una pared de
potencial infinito. Ahora lo emplearemos para hallar soluciones en el
contínuo.