Práctica Computacional:
La Ecuación de Schrödinger
Partícula confinada en un pozo de potencial unidimensional
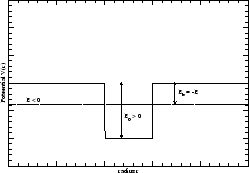
La figura 1 representa un
``pozo de potencial" unidimensional
(1-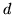 potential well)
potential well)
Resolver la Ecuación de Schrödinger y obtener el espectro de
energías posibles del sistema.
Figure 1:
Pozo de potencial unidimensional, de ancho 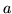 .
.
 |
Procedimiento de solucion: separar el problema en distintos sectores,
solucionarlos independientemente y hacer coincidir las funciones (y sus
derivadas) en los bordes.
Se debe solucionar separadamente el caso de soluciones pares e impares.
En el sector I (adentro del pozo) reemplazar:
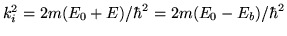 y
y
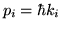
En el sector II (afuera del pozo) reemplazar:
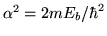 y
y
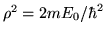
la continuidad de las funciones y sus derivadas llevaran a
obtener ecuaciones trascendentales de la forma:
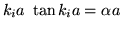 para el caso par
para el caso par
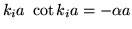 para el caso impar
para el caso impar
NO INTENTE RESOLVERLAS !
Una forma de resolver este problema es graficando:
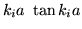 ó
ó
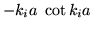
Las soluciones posibles se encuentran en las intersecciones de esta funcion con
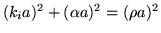
- Utilizar el gráfico dado en la Figura 2 y
calcular el primer estado ligado impar, para el caso en que
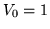 a.u. y
a.u. y 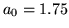 a.u..
a.u..
- Trazar un boceto de las primeras soluciones y
compararlas con las del pozo infinito.
- Analice el problema de una partícula en un pozo de potencial
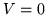 (
(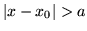 ) y
) y 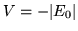 (
(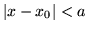 ).
).
- Cómo cambian las energías si en lugar de
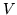 se utiliza
se utiliza
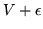 ?
?
- Cómo cambian las energías si en lugar de tener un potencial de
rango
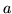 , este es
, este es 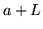 ?
?
- Las expresiones de las energías que se obtienen en estos ejercicios
son exactas (no hay
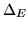 ). Qué se puede decir acerca del tiempo
que tarda una partícula en decaer desde un estado excitado?
). Qué se puede decir acerca del tiempo
que tarda una partícula en decaer desde un estado excitado?
- En las siguientes figuras están representados un potencial unidimensional,
la función de onda radial correspondiente al 5
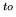 nivel de una
partícula en ese potencial, y su energía correspondiente.
Sólo uno de los gráficos es correcto. Identificar cuál es.
nivel de una
partícula en ese potencial, y su energía correspondiente.
Sólo uno de los gráficos es correcto. Identificar cuál es.
- En las figuras siguientes están representados potenciales
unidimensionales, y sus estados fundamentales, desplazados verticalmente
con su energía correspondiente.
Cada función de onda es solución de alguno de los potenciales
dibujados en la figura.
Identificar cuál de estos gráficos es el correcto.
Figure:
Curva 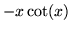 .
.
 |
Solución de la caja de potencial utilizando Mathematica
1) Autofunciones del potencial
Definicion del ancho y la profundidad y la ubicacion del pozo
![RowBox[{RowBox[{Clear[V0, R0, Del, x0] ;, , RowBox[{RowBox[{V0, =, , 5.}], ;}], ɯ ... #62371;, Poten[r_] = If[r> (R0 - Del/2), -V0, 0] * If[r< (R0 + Del/2), 1, 0] ;}], }]](HTMLFiles/well_1.gif)
![Plot[Poten[r], {r, 0, 10}] ;](HTMLFiles/well_2.gif)
![[Graphics:HTMLFiles/well_3.gif]](HTMLFiles/well_3.gif)
Soluciones pares
Busqueda de las energias
(* Cell -> Convert To = Input Form *)
Plot[{ξ*Tan[ξ], Sqrt[γ^2 - ξ^2]}, {ξ, 0, γ}, PlotRange -> {0, γ}];
![[Graphics:HTMLFiles/well_4.gif]](HTMLFiles/well_4.gif)
(* Cell -> Convert To = Traditional Form *)
![Plot[{ξ tan(ξ), (γ^2 - ξ^2)^(1/2)}, {ξ, 0, γ}, PlotRange ... 371;BackgroundRGBColor[0, 1, 1], AxesLabel {ξ, "γ"}] ;](HTMLFiles/well_5.gif)
![[Graphics:HTMLFiles/well_6.gif]](HTMLFiles/well_6.gif)
![RowBox[{RowBox[{FindRoot, [, RowBox[{{ξ Tan[ξ] η, ξ^2 + η^2γ^2}, ,, RowBox[{{, RowBox[{ξ, ,, 1.4}], }}], ,, {η, .5}}], ]}], }]](HTMLFiles/well_7.gif)
![RowBox[{{, RowBox[{RowBox[{ξ, , 1.3549}], ,, RowBox[{η, , 6.17772}]}], }}]](HTMLFiles/well_8.gif)

Definicion de los coeficientes
![Clear[kr, κ] RowBox[{k, =, , RowBox[{2, , *, , RowBox[{1.3549, /, Del}]}]}] RowBox[{κ, , =, , RowBox[{2, *, , RowBox[{6.17772, /, Del}]}]}]](HTMLFiles/well_10.gif)
![Clear[A] ; A = ^(-κ (Del/2))/Cos[k (Del/2)] ;](HTMLFiles/well_11.gif)
Definicion de las soluciones pares
![Clear[solp, C2, Normapar] solp[r_] = If[r<R0 - Del/2, ^(κ (r - R0)), If[r<R0 + Del/2, A Cos[k (r - R0)], ^(-κ (r - R0))]] ](HTMLFiles/well_12.gif)
![C2 = NIntegrate[ (solp[r])^2 , {r, 0, Infinity}] ; Normapar = 1/Sqrt[C2] ;](HTMLFiles/well_13.gif)
![Plot[{Poten[r], Normapar * solp[r]}, {r, 0, 10}, PlotRange {-1, 1}] ;](HTMLFiles/well_14.gif)
![[Graphics:HTMLFiles/well_15.gif]](HTMLFiles/well_15.gif)
Soluciones impares
Busqueda de las energias
![Plot[{-ξ Cot[ξ], (γ^2 - ξ^2)^(1/2)}, {ξ, 0, γ}, PlotRange {0, γ}] ;](HTMLFiles/well_16.gif)
![[Graphics:HTMLFiles/well_17.gif]](HTMLFiles/well_17.gif)
Created by
Mathematica
Darío Mitnik
U.B.A.
![RowBox[{RowBox[{Clear[V0, R0, Del, x0] ;, , RowBox[{RowBox[{V0, =, , 5.}], ;}], ɯ ... #62371;, Poten[r_] = If[r> (R0 - Del/2), -V0, 0] * If[r< (R0 + Del/2), 1, 0] ;}], }]](HTMLFiles/well_1.gif)
![]()
![[Graphics:HTMLFiles/well_3.gif]](HTMLFiles/well_3.gif)
![[Graphics:HTMLFiles/well_4.gif]](HTMLFiles/well_4.gif)
![Plot[{ξ tan(ξ), (γ^2 - ξ^2)^(1/2)}, {ξ, 0, γ}, PlotRange ... 371;BackgroundRGBColor[0, 1, 1], AxesLabel {ξ, "γ"}] ;](HTMLFiles/well_5.gif)
![[Graphics:HTMLFiles/well_6.gif]](HTMLFiles/well_6.gif)
![]()
![]()
![]()
![]()
![Clear[A] ; A = ^(-κ (Del/2))/Cos[k (Del/2)] ;](HTMLFiles/well_11.gif)
![Clear[solp, C2, Normapar] solp[r_] = If[r<R0 - Del/2, ^(κ (r - R0)), If[r<R0 + Del/2, A Cos[k (r - R0)], ^(-κ (r - R0))]] ](HTMLFiles/well_12.gif)
![]()
![]()
![[Graphics:HTMLFiles/well_15.gif]](HTMLFiles/well_15.gif)
![]()
![[Graphics:HTMLFiles/well_17.gif]](HTMLFiles/well_17.gif)