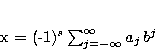Representación de Números

Representación Numérica en una base

Dado un número , su representación en una dada base consiste en escribirlo como

$\begin{displaymath} x = (-1)^{s} \sum_{j=-\infty}^{\infty} a_{j} b^{j} \end{displaymath}$

(1)

donde el signo es igual a 0 o 1 y los coeficientes $a_{j}$ son enteros positivos menores que . En la vida real la suma tiene sólo un número finito de términos por lo que algunos números son sólo representados en forma aproximada. Usualmente, utilizamos el sistema decimal de numeración () pero la representación numérica en sistemas digitales se realiza en general en base 2, denominado sistema de numeración binaria, y ocasionalmente en base 16 (sistema hexadecimal). Los números se representan en memoria como una cadena de bits que pueden tomar los valores 0 ó 1. Se denomina byte a un grupo de 8 bits consecutivos.

Representación de números enteros

En representación binaria un número entero se escribe como

$\begin{displaymath} n = a_{0} 2^{0} + a_{1} 2^{1} + a_{2} 2^{2} + a_{3} 2^{3} + \dots \end{displaymath}$

(2)

donde cada coeficiente $a_{j}$ es igual a 1 o 0. Usualmente los números enteros ocupaban 4 bytes de memoria (32 bits), aunque en las computadoras modernas se pueden utilizar enteros de 64 bits. Los números que pueden almacenarse en la representación de 4 bytes están en el rango:

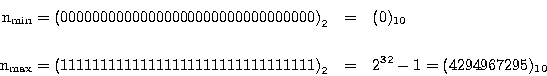
$\begin{eqnarray*} \mathrm{n_{min}} = \left( 00000000 00000000 00000000 00000000... ...1 11111111 11111111 \right)_{2} &=& 2^{32}-1 = (4294967295)_{10} \end{eqnarray*}$

para números enteros sin signo. Si se utiliza el primer bit de la izquierda como signo (0, positivo; 1, negativo) el rango se reduce a $n_{min} = -2147483648$ y $n_{max} = 2147483647$ para enteros con signo.

Representación de números reales

Las computadoras, con un número finito de bits, no pueden almacenar todos los números reales en forma exacta. Esto es similar a lo que ocurre con los números irracionales (como $\pi$ , $\sqrt{2}$ , etc) o periódicos (, , ...) en el sistema decimal. La forma convencional de almacenar números reales en la memoria de una computadora es mediante el método llamado de punto flotante o floating point. Uno de los sistemas más comunes es la representación de números reales en simple precisión utilizada en la convención IEEE. En dicho sistema cada número de precisión simple ocupa 4 bytes (32 bits) que se destinan a: el signo (1 bit), un exponente (8 bits) y la parte fraccionaria de la mantisa (23 bits)¹. De esta manera un número está determinado por estas tres cantidades

$\begin{displaymath} x = (-1)^{s} \times \; 2^{\mathrm{exp} - E}\; \times 1.\mathrm{mantisa} \end{displaymath}$

(3)

En esta representación, los 8 bits utilizados permiten que el exponente se encuentre en el rango $0 < \mathrm{exp} < 255$ . Se utiliza la constante para también obtener resultados negativos ². Observe que para ganar un bit, se omite la parte entera de la mantisa que se supone igual a 1. Esta representación se llama normalizada y se utiliza para todos los números, excepto aquellos muy grandes o muy pequeños. En particular, esta convención no permite representar el número 0.

Algunos ejemplos

Para aclarar los conceptos, consideremos algunos ejemplos de números normalizados en precisión simple:

$\displaystyle (\underbrace{0} \underbrace{1 0 0 0 0 0 1 1} \;(1),\; \u... ...race{0 0 1 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0})_{2}$	$\textstyle =$	$\displaystyle (19.765625)_{10}$
$\displaystyle \mathrm{signo}\;\; \mathrm{exponente}\qquad \qquad \qquad \qquad \mathrm{mantisa}\hphantom{(0 0 0 1 0 1 1 ,1 0)}$			(4)
$\displaystyle (1)_{10} \qquad (131)_{10} \qquad \qquad \qquad \qquad (241/1024)_{10} \hphantom{(0 1 1 1 0 1 0 )}$

Hemos representado entre paréntesis la parte entera de la mantisa (que es igual a 1 siempre por convención. Debe notarse que el número final se obtiene considerando que:

El signo es positivo (bit de signo igual a 0).
El exponente se obtiene como 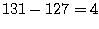, que en sistema decimal da $2^{4}=16$ .
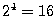La mantisa 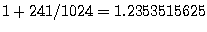se obtiene sumando: 1 (implícito), 1/8, 1/16, 1/32, 1/64 y 1/1024.

Como segundo ejemplo veamos la conversión inversa, del número $(3.375)_{10}$ a sistema binario. El bit de signo es 0. El número puede expresarse como la fracción y es mayor que 2 por lo que debemos sacar un exponente positivo; en este caso, factorizamos por $2^{1}$ y nos quda que puede escribirse como

$\begin{displaymath} \frac{27}{16} = \frac{1}{1} + \frac{1}{2} + \frac{0}{4} + \frac{1}{8} + \frac{1}{16} \end{displaymath}$

por lo que, después de eliminar la parte entera y agregando el signo y el exponente, el número es:

$\begin{displaymath} (3.375)_{10} = (0 \; 1 0 0 0 0 0 0 0 \;(1), 1 0... ... 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 )_{2} \end{displaymath}$

Aritmética con números binarios

Una de las consecuencias más importantes de usar una representación de punto flotante (con signo, mantisa y exponente) es que dos números deben tener el mismo exponente para poder ser sumados o restados. Consideremos por ejemplo la suma de los dos números anteriores y en sistema binario

		$\displaystyle (0 \; 1 0 0 0 0 0 1 1 \;(0), 0 0 1 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 )_{2}$
	$\textstyle +$	$\displaystyle \underline{(0 \; 1 0 0 0 0 0 1 1 \; (1), 0 0 1 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 )_{2}}$
		$\displaystyle (0 \; 1 0 0 0 0 0 1 1 \; (1), 0 1 1 1 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 )_{2}$

Aquí hemos cambiado a una forma no normalizada para utilizar el mismo exponente en ambos números. Este procedimiento disminuye la cantidad de dígitos significantes.

Casos particulares y otros ejemplos

¿Qué pasa cuándo el número es exactamente cero?.

La convención dice que se interpreta exactamente cero cuando todos los bits son 0. Esto significa, No sólo los de la mantisa sino también los del exponente. Nótese que para números de 64 bits (8 bytes) se interpreta que el número $10^{-127} \equiv 0$ , ya que el exponente ha sido corrido en 127.

Representación de infinitos varios

Hay dos tipos de infinitos: positivos y negativos. La convención para representar estos números dice que un número se considera infinito si cada uno de los bits del exponente es 1 y los de la mantisa son 0. El signo permite distinguir entre $+\infty$ y $-\infty$ .

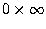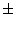Otro caso particular en la convención es cuando necesitamos representar algo que no corresponde a un número bien definido ( $0 \times \infty$ , por ejemplo). El resultado de estas operaciones no son números (uno obtiene algo como $\pm$ NaN) y la representación interna corresponde a todos los bits del exponente en 1 y además al menos uno de la mantisa es 1 también.

Ejercicios

Table 1: Representación de números de punto flotante en simple y doble precicsión.

Propiedad	Simple precisión	Doble precisión
Mayor número representable	3.402823466 10 $^{38}$	1.7976931348623157 10 $^{308}$
Menor número sin pérdida de precisión	1.175494351 10 $^{-38}$	2.2250738585072014 10 $^{-308}$
Menor númer representable	1.401298464 10 $^{-45}$	5 10 $^{-324}$
Bits de mantisa	23	52
Bits de exponente	8	11
Epsilon	1.1929093 10 $^{-7}$	2.220446049250313 10 $^{-16}$

En notación hexadecimal (base 16) cada símbolo representa un conjunto de cuatro bits (rango de 0 a 15). Algunos casos especiales son:

0	0x00000000
1.0	0x3f800000
0.5	0x3f000000
3	0x40400000
+inf	0x7f800000
-inf	0xff800000
+NaN	0x7fc00000 or 0x7ff00000

Referencias

Understanding Floating Point Numbers by Jeff Bezanson en http://www.cprogramming.com/advtutorial.html.

Footnotes

... bits)¹

En doble precisión se utilizan 64 bits (8 bytes): 1 para el signo, 11 bits para el exponente y 52 bits para la mantisa

... negativos ²

En rigor, en la convención IEEE-754 el exponente varía en el rango [-126,127] y se reservan los restantes valores para representar números muy pequeños y muy grandes