Polinomios de Lagrange
Interpolar por este método consiste en construir un polinomio Pn(x) de grado máximo n, que pasa por n+1 puntos dados. La función f(x) tabulada en n+1 puntos xk es:
f(xk) = Pn(xk) para todo k=0,1,2,...,n |
El polinomio Pn(x) está dado por una combinación de los respectivos Polinomios de Lagrange Ln,k(x)
Pn(x) = f(x0)Ln,0(x) + f(x1)Ln,1(x) + ... + f(xn)Ln,n(x) |
y los polinomios de Lagrange se definen como:
(x-x0)(x-x1)....(x-xk-1)(x-xk+1)....(x-xn)
Ln,k(x) = -------------------------------------------
(xk-x0)(xk-x1)..(xk-xk-1)(xk-xk+1)..(xk-xn)
|
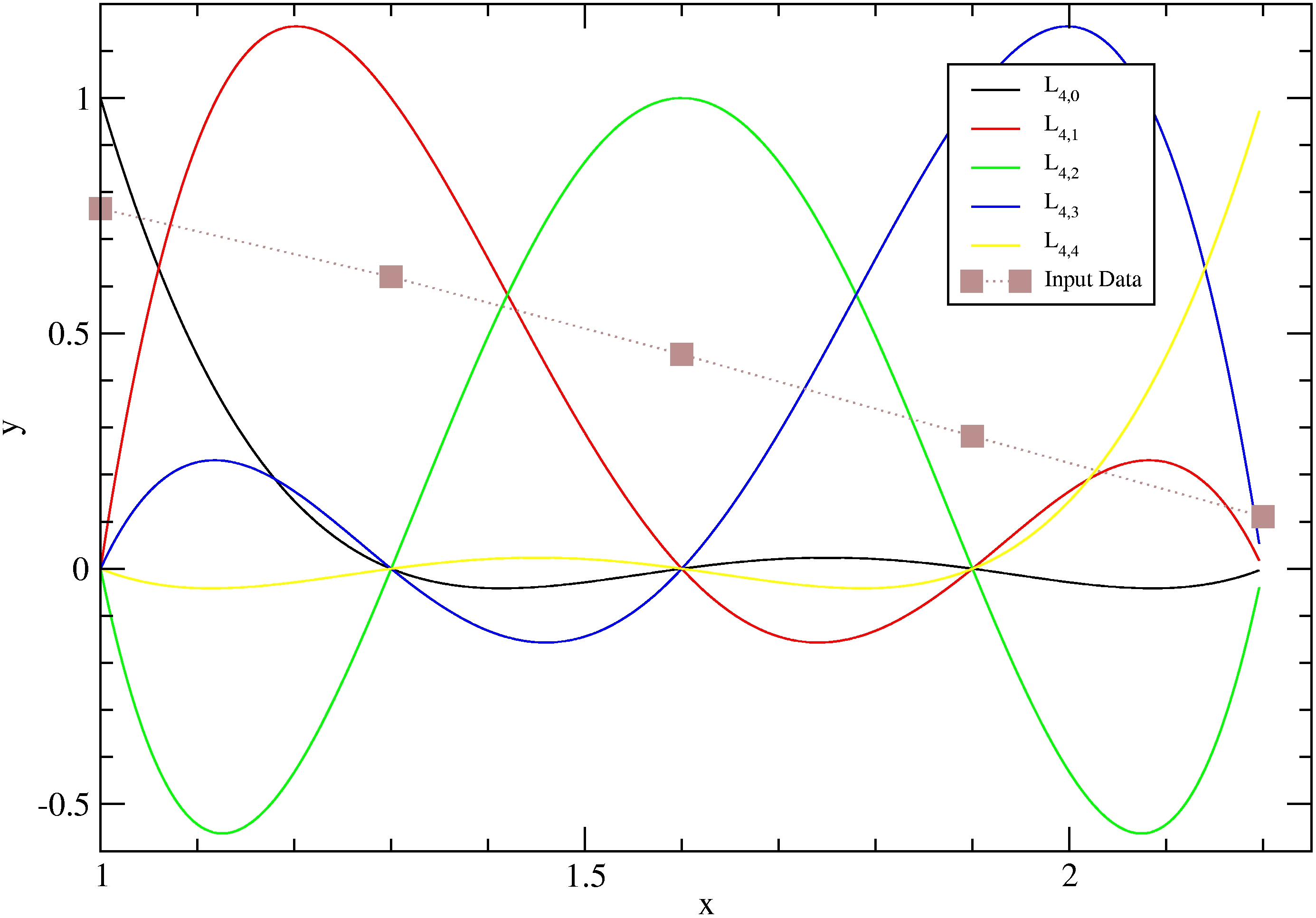
Como ejemplo vemos los 5 polinomios de Lagrange que pasan por los puntos x= 1.0, 1.3, 1.6, 1.9 y 2.2:
El error dado por éste método de interpolación es:
f(x) - Pn(x) = Rn(x) = (1/(n+1)!) f(n+1)(ξ)(x - x0)(x - x1) ... (x - xn) |