Gases
Práctica de Física 2 (biólogos y geólogos) - Sigman returns - 2o cuatrimestre de 2008 http://www.df.uba.ar/users/gsolovey/fisica2/fisica2.html
Contenidos
Scripts (archivos .m)
Todo lo que aprendimos hasta ahora de Matlab son instrucciones que se pueden ejecutar desde la línea de comandos >>. Sin embargo, muchas veces es muy útil armar scripts, que son pequeños programitas o secuencias de instrucciones de Matlab. Estos scripts, que en Matlab tienen la extensión .m, se pueden editar, guardar y ejecutar cuando quieran. Es decir, un script .m es un programa escrito en código Matlab. Los ejercicios que hagan en la clase se los pueden llevar guardados en un archivo .m.
Matlab viene con un editor de scripts con varias funciones muy útiles que van a ir descubriendo. Para abrirlo, pueden tipear >> edit o bien usar el menú File >> New >> M-file. Esto abre un editor donde en cada línea ponemos una instrucción.
Integración numérica
En este ejercicio vamos a integrar la función
![]()
Esta función se pueden integrar analíticamente. Es cierto que es un poco tedioso hacerlo a mano pero también pueden hacerlo con ayuda de algún programa como el Mathematica que de hecho tiene una página donde se pueden integrar funciones:
Para integrar numéricamente, vamos a hacer con un método muy crudo pero que funciona. Como ya sabemos, la integral se puede ver geométricamente como el área bajo la curva de la función. Entonces, vamos a dividir el intervalo de integración en pequeños intervalitos y aproximamos la función en cada uno de ellos por una constante (el valor de la función en el punto medio del intervalo). Finalmente, la integral se calcula simplemente sumando las áreas de todos los intervalos.
![]()
donde:
![]()
![]()
![]()
El siguiente código calcula la integral entre x=-3 y x=2.5 con un N=15.
a) Guárdenlo en un archivo .m y repitan el cálculo con diferentes valores de N.
b) Grafiquen el resultado en función de N, o sea, grafiquen I(N) y sobre el mismo gráfico la solución exacta (*). Analicen el resultado determinando un número suficiente de N para que el error de la integral sea menor que 0.03 (en valor absoluto).
(*): El resultado de la integral calculado de forma analítica es I=37.5048.
clear xi x fi f dx x1=-3; % define los límites de integración x2=2.5; N=15; % define el número de intervalos que vamos a usar dx=(x2-x1)/N; % calcula el ancho de cada intervalo % acá definimos los vectores x y f para la integración. Tomamos valores de % x en la posición media de cada intervalo. xi = (x1+dx/2):dx:(x2-dx/2); % verifique que esta definición coincide con % la que dimos arriba fi = (xi-2).*(xi+1).*xi.*(xi+2.5).*cos(2*xi)+5; % definimos f(xi) % Calculamos la integral. La instrucción |sum| calcula la suma de todos los % elementos de un vector. Entonces basta con multiplicar el vector |fi| % (altura de cada rectángulo) por |dx| (la base de cada rectángulo) y luego % sumar las componentes de ese vector. I=sum(fi*dx); % Graficamos con barras la aproximación a la función ... h=bar(xi,fi); set(h,'FaceColor', 'w', 'EdgeColor', 'r', 'BarWidth', 1, 'LineWidth', 1); hold on % ... y con línea negra gruesa la función (para esto definimos un vector |x| % con muchos puntos. x = x1:0.01:x2; f = (x-2).*(x+1).*x.*(x+2.5).*cos(2*x)+5; plot(x,f,'k', 'LineWidth', 2); axis([-3.5 3 0 25]) % redefinimos los límites del eje x y del y, % respectivamente. xlabel('x'); ylabel('y'); legend('aproximación','f(x)') hold off
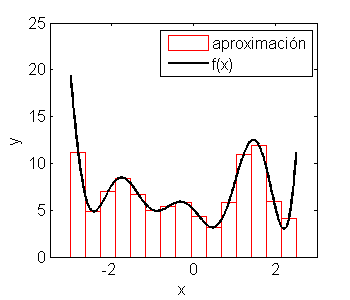
Análisis de la ecuación de estado de un gas
Un grupo de investigadores hizo un experimento (**) para estudiar las propiedades termodinámicas de un gas. El experimento consiste en medir la presión que ejerce el gas para distintos volumenes manteniendo la temperatura constante.
En un experimento con vapor de agua a T = 712 K variaron el volumen de un mol de gas entre 0.045 l y 0.915 l. Amablemente nos dieron los resultados de su experimento para que lo analicemos en la materia. Los datos están en el archivo gas.txt que pueden bajar de acá:
http://www.df.uba.ar/users/gsolovey/fisica2/Matlab_Gases/gas.txt
Si guardan ese archivo en una carpeta, después lo pueden importar al matlab con la instrucción load:
close all clear all load gas.txt
Si funcionó, tendrán una nueva variable de Matlab que se llama gas y tiene dos columnas. Esto lo pueden verificar con la instrucción whos que da la lista de variables que ya definieron y su tamaño (o también en la ventana Workspace). Vean que el tamaño de la matriz gas es de 115 x 2 (filas x columnas).
Puede explorar el contenido de la misma haciendo doble-click en el nombre de la variable (dentro de la pestaña Workspace) o bien escribiendo gas en la ventana de comandos.
La primera columna corresponde al volumen (en litros) y la segunda a la presión (en atm). Podemos definir esas dos variables con otro nombre para no usar la variable gas para las dos cosas.
V=gas(:,1); % esto asigna a la variable V todos los valores de la primera columna de gas P=gas(:,2); % lo mismo con la segunda columna para la variable P
a) Grafiquen P vs. V usando símbolos para cada punto experimental. Sobre los datos experimentales, grafiquen la función que esperarían obtener (para la temperatura del experimento) si fuera un gas ideal.
b) En un nuevo gráfico, muestren el error relativo entre los datos experimentales y la expresión del gas ideal.
![]()
Ayuda: Para definir el error relativo busquen en el Help de Matlab la función que calcula el valor absoluto.
¿Cuál es el error relativo máximo? ¿Para qué valor de volumen ocurrió? Ayuda: En este caso pueden determinarlo con la función Data Cursor que tiene un ícono en la ventana de la figura. O bien pueden explorar la función max y luego la función find desde la línea de comandos.
c) Si el error relativo máximo es mayor que el 30%, podemos considerar que el gas no es ideal, o mejor dicho, que para esas condiciones el gas no se comporta como ideal. Una variante del gas ideal es la ecuación de van der Waals:
![]()
que tiene dos parámetros: a y b. ¿Qué significan cada uno? Para el vapor de agua, esos parámetros son
![]()
![]()
Además, recuerden que
![]()
Grafiquen la isoterma de T = 712 K de la ecuación de estado de van der Waals. ¿Cuál es el error relativo máximo entre los datos experimentales y lo esperado según la ecuación de van der Waals?
d) Determine a qué temperatura mínima tendría que estar el gas para que la aproximación de gas ideal sea una buena descripción para V > 1 litro, digamos con un error relativo menos al 5%. O sea, ¿a qué temperatura un gas de van der Waals se parece a un gas ideal (para volúmenes mayores que 1 litro)?
e) Ahora los científicos quieren hacer una experiencia de expansión isotérmica con este gas a una nueva temperatura de T = 800 K partiendo desde un volumen de V1 = 0.05 litros hasta uno de V2=2 litros. Se preguntan cuál es el trabajo que haría el gas en la expansión. ¿Pueden responder esa pregunta (calculando numéricamente)? Recuerden que:
![]()
En función de lo contestado en el punto anterior, ¿deben usar la ecuación de van der Waals o pueden usar la del gas ideal?
(**): Por si hace falta aclararlo, en este ejercicio el experimento es ficticio. La idea es que puedan ir desarrollando herramientas computacionales, el tipo de cosas que se pueden hacer con Matlab y las preguntas que surgen cuando uno analiza datos.
Ciclo de Carnot
Considere una máquina que opera según el ciclo de Carnot entre las temperaturas T1=4 y T2=6 utilizando un gas ideal. El primer tramo del ciclo es una expansión isotérmica desde el volumen inicial (V1=6.5) hasta un volumen V2=8.5 a la temperatura T2. Nota: en este problema usamos unidades arbitrarias.
a) Grafique las dos isotermas con diferentes colores.
b) Encuentre la presión y el volumen de los 4 estados "extremos" del ciclo (donde se cruzan las adiabáticas con las isotermas).
c) Grafique el ciclo completo de Carnot (*)
d) Calcule el trabajo que entrega el sistema en todo el ciclo (puede hacerlo numéricamente). Calcule ahora el trabajo que haría el gas en un ciclo de van der Waals en el que V2=10.5 (o sea, se expande el doble)
(*): En los tramos adiabáticos cambia la temperatura. Para dar cuenta de ese cambio se puede usar una escala de colores. En el archivo .m que pueden encontrar en el siguiente link, está explicada la forma de hacerlo en matlab con la instrucción scatter. Revisen ese código y úsenlo para graficar las adiabáticas: http://www.df.uba.ar/users/gsolovey/fisica2/Matlab_Gases/adiabaticas.m
-------------------------------------------------------- http://www.df.uba.ar/users/gsolovey/fisica2/fisica2.html