Introducción a Matlab
Práctica de Física 2 (biólogos y geólogos) - Sigman returns - 2o cuatrimestre de 2008 http://www.df.uba.ar/users/gsolovey/fisica2/fisica2.html
Aclaración: Todo el texto que está dentro de las cajas grises lo pueden copiar y pegar dentro de la ventana "Command Window" de Matlab porque son instrucciones para ejecutar.
Contenidos
Cantidades escalares y variables
Los siguientes dos comandos le asignan un número a dos variables: a y b. En Matlab, todo lo que está después del signo % es un comentario y no es leído como una instrucción de Matlab.
a=3 % le asigna a la variable a el número 3 b=4; % le asigna a la variable b el número 4 y al usar el *;* al final % no imprime la salida en pantalla
a =
3
Las siguientes son algunas operacione posibles con variables
c = a + b; % suma d = a / b; % cociente e = a^b; % potencia f = sqrt(b); % raíz cuadrada
A veces es útil reasignar el valor de una variable a partir del valor que tenía antes. Por ejemplo:
a = a + 2 % le asigna a la variable a el valor que tenía a antes más 2.
a =
5
Pueden ejecutar varias veces la instrucción anterior que le va a ir sumando 2 al valor de a en cada paso
a = a + 2 a = a + 2 a = a + 2
a =
7
a =
9
a =
11
El uso de los paréntesis. Hacer las siguientes cuentas a mano y comparar con los resultados obtenidos en Matlab
a + b / 2; (a + b) / 2; b / f - 1; b / (f - 1);
Vectores
En Matlab se usan mucho los arreglos de números, que se llaman vectores si se trata de una fila de números o matrices si se trata de arreglos de filas y columnas. En esta guía empezamos con los vectores.
Hay diferentes formas de definir vectores en Matlab. Por ejemplo, las siguientes expresiones son equivalentes para definir vectores. Pruébelo.
v1 = [1 2 3 4 5 6 7 8 9 10];
v2 = 1:10; % define un vector que empieza en 1 hasta el 9 de pasos de a 1
w1 = [2 4 6 8 10 12 14 16 18 20];
w2 = 2:2:20; % define un vector que empieza en 2 hasta el 10 de pasos de a 2
Las siguientes son algunas operaciones entre vectores. Vea los resultados de cada una.
z0 = w1 + 2; % le suma 2 a cada componente del vector w1 z1 = w1 - v1; % resta componente a componente los dos vectore z2 = w1 + w2; % suma z3 = w1.^2; % eleva al cuadrado cada uno de los elementos de w1 z4 = sqrt(w2); % calcula la raíz cuadrada de cana elemento de w1 z5 = w2 ./ v2; % divide w2 por v2 elemento a elemento
Gráficos
Hay varios comandos para graficar funciones en Matlab. Entre ellas, plot, area, bar, stairs.
Empezamos graficando la función usando plot
![]()
Para esto primero tenemos que definir los valores de x que vamos a usar. Por ejemplo, si queremos usar x=0,1,2,3,...10 hacemos lo siguiente:
x = 0:10;
A los valores de la función los vamos a guardar en el vector y. Para eso hacemos lo siguiente:
Noten que para elevar al cuadrado cada elemento de x es necesario usar la operación .^. Si se usa la operación ^ entre dos vectores lo que se obtiene es el producto escalar entre los dos, como veremos más adelante.
y = 2*x.^2 + 3*x - 5; figure plot(x,y)
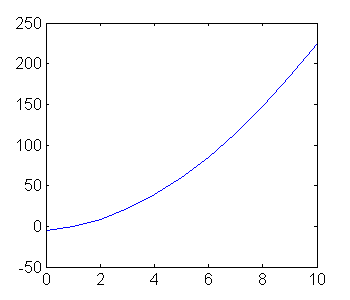
Podemos volver a graficar la misma función pero en otro intervalo. Por ejemplo para x entre -5 y 5.
x = -5:5; y = 2*x.^2 + 3*x - 5; plot(x,y,'-+'); % grafica con línea y símbolos
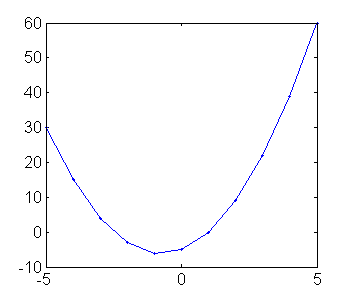
Y si queremos usar más puntos para graficar, podemos tomar un vector x con más elementos, por ejemplo:
x = -5:0.2:5; % esto genera un vector que empieza en -5 y va hasta 5 de a pasos de 0.2 y = 2*x.^2 + 3*x - 5; plot(x,y,'-+')

Pueden probar repetir la última instrucción reemplazando el uso de plot por area(x,y) o stairs(x,y) para ver qué hace.
Ahora graficamos las siguientes funciones.
![]()
![]()
clear all % borra todas las variables definidas hasta ahora x = 0.1:0.01:5; % creamos el vector x f = log(x); % crea un vector que en cada componente tiene el logaritmo de cada elemento de |x|. g = exp(x); % lo mismo con la exponencial plot(x,f); % grafica la función f(x) grid on figure % crea una nueva figura plot(x,g) grid on
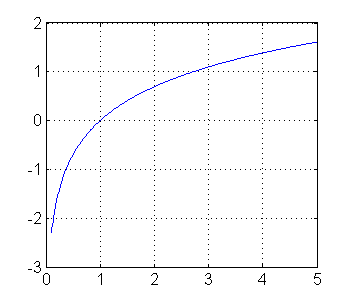
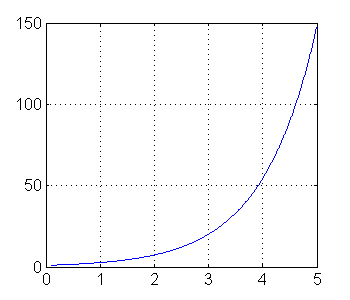
Para crear un gráfico con 2 figuras usando subplots y arreglarlos un poco:
FS = 15; % define el tamaño de las letras que vamos a usar figure subplot(1,2,1) plot(x,f,'--r','LineWidth',2) xlabel('x','FontSize',FS) ylabel('log(x)','FontSize',FS) set(gca,'FontSize',FS); % define el tamanio de las letras de los ejes subplot(1,2,2) plot(x,g,'--k','LineWidth',2) xlabel('x','FontSize',FS) ylabel('exp(x)','FontSize',FS) set(gca,'FontSize',FS);
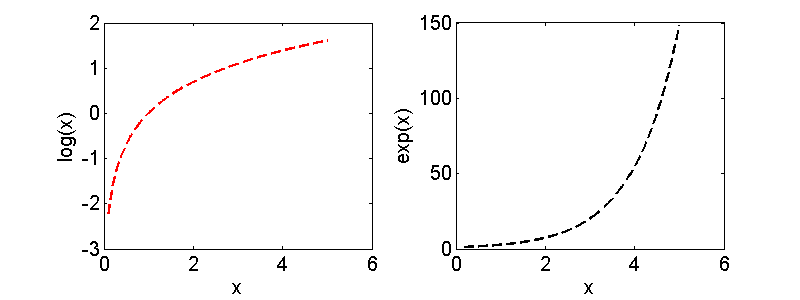
Graficar varias funciones en una misma figuras usando subplots.
FS = 15; % definimos el tamaño de letra que vamos a usar t=1:1000; % definimos el tiempo como un vector de 1 a 1000 con incrementos de a 1 figure; set(gcf,'Color','w'); % define el color del fondo subplot(2,2,1); % divide la figura en 4 regiones (2 filas y 2 columnas y % empezamos definiendo el gráfico 1 plot(t,cos(t/50)); xlabel('t','FontSize',FS); %pone títulos al eje x ylabel('x','FontSize',FS); %pone títulos al eje y grid on; %agregamos una grilla title('Coseno'); %título del gráfico % Podemos dar todas las instrucciones en una única línea separadas por ; subplot(2,2,2);plot(t,exp(-t/150));xlabel('t','FontSize',FS);ylabel('x','FontSize',FS);grid on;title('Exp'); subplot(2,2,3);plot(t,sin(t/50).*cos(t/50));xlabel('t','FontSize',FS);ylabel('x','FontSize',FS);grid on;title('Seno*Coseno'); subplot(2,2,4);plot(t,1./(1+(t/150)));xlabel('t','FontSize',FS);ylabel('x','FontSize',FS);grid on;title('1/(1+t)');
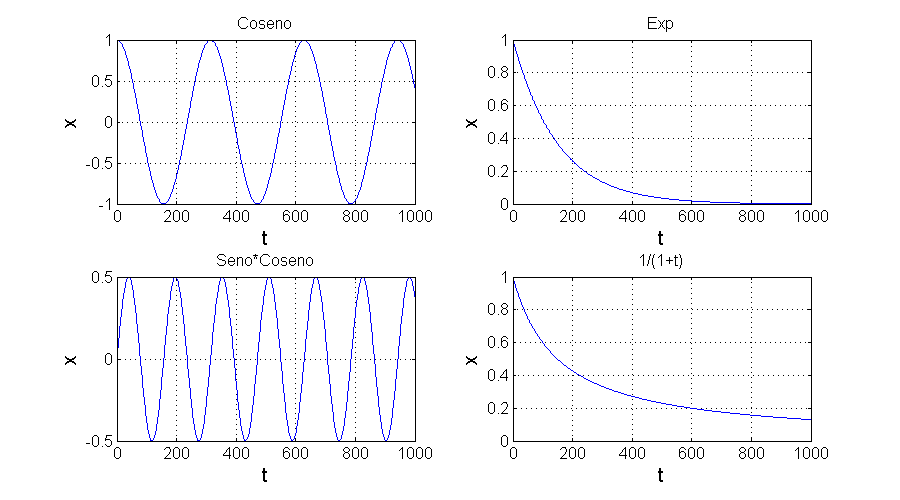
Para terminar mostramos cómo graficar una función usando el comando area y graficamos con distinta cantidad de puntos. Vean la importancia de tener suficientes puntos para graficar una función que varía en el tiempo.
figure
subplot(1,2,1)
dx=2; % definimos dx que será el paso del vector x
x=-5:dx:15; % definimos el vector x que toma valores espaciados en dx
y=sin(2*x).*cos(1.2*x+2)+2;
area(x,y) % podríamos reemplazar esto por |plot(x,y)| o |plot(x,y,'+-')|
subplot(1,2,2)
dx=0.1; %definimos dx como el paso del vector x.
x=-5:dx:15;
y=sin(2*x).*cos(1.2*x+2)+2;
area(x,y)% podríamos reemplazar esto por |plot(x,y)| o |plot(x,y,'+-')|
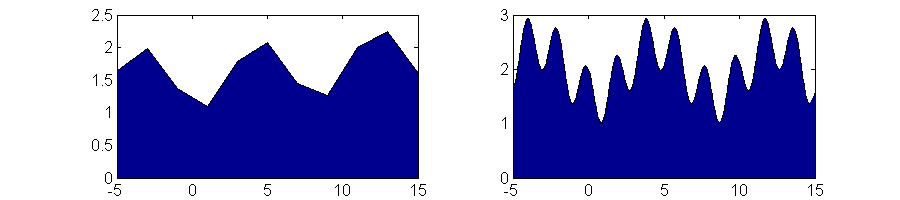
Ejercicios
1) Frecuencia de muestreo. Queremos representar en un gráfico a una variable que cambia en el tiempo de acuerdo a la ecuación
![]()
El siguiente código define la función en un rango de valores de t.
clear t y dx dt=1; t=-pi:dt:pi; y=1.2*cos(2*t)+0.8*sin(1.2*t)+3;
Grafique la función usando plot (y luego area) y pruebe con distintos valores de dt hasta encontrar uno que sirva para representar adecuadamente la función.
2) El siguiente código grafica la función
![]()
clear x y x = -2:0.1:2; y = 9-x.^2; figure plot(x,y)
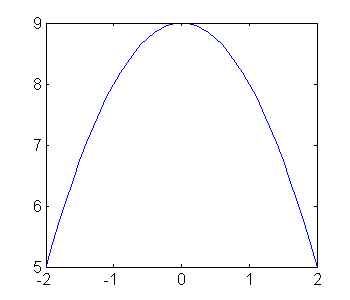
Modificarlo para graficar la función
![]()
3) La ecuación de los gases ideales es
![]()
En este problema trabajamos con variables 'adimensionales' y tomamos por simplicidad NK = 1. Grafique la presión en función del voluúmen para dos temperaturas diferentes en el mismo gráfico y con colores distintos. Póngale nombre a los ejes.
Ayuda: Para graficar dos funciones en el mismo gráfico use el comando hold. Por ejemplo, si después de graficar una función, entramos hold on eso "congela" la figura y lo que grafiquemos a continuación será superpuesto hasta que escribamos el comando hold off.
4) Graficar en la misma figura las siguientes funciones
![]()
Decidir el número de puntos que van a usar para obtener una curva suave
5) Gaussiana. Definir los parámetros de la función y graficarla en un rango de valores de x adecuado.
![]()
6) Graficar una función exponencial para distintos valores de los parámetros en el mismo gráfico
![]()
-------------------------------------------------------- http://www.df.uba.ar/users/gsolovey/fisica2/fisica2.html