Psicofísica - Random walks en el bocho (indebrein)

Práctica de Física 2 (biólogos y geólogos) - Sigman returns - 2o cuatrimestre de 2008 http://www.df.uba.ar/users/gsolovey/fisica2/fisica2.html

Objetivo: Analizar los resultados de los experimentos psicofísicos hechos en clase. En el experimento el sujeto tenía que mirar un conjutno de partículas que hacía una caminata al azar en una pantalla. Entre ellas, había un grupo de partículas que hacían un movimiento "coherente", sólo se movían en la dirección horizontal (o bien hacia la izquierda o bien hacia la derecha). El objetivo era responder hacia qué dirección se mueven las partículas coherentes.

Se trata de un experimento de toma de decisiones entre dos opciones a partir de evidencias o estímulos visuales. En cada experimento se tenía un porcentaje diferente de partículas que se movían coherentemente (grado de coherencia), elegidos entre 4 valores prefijados. También al azar se eligió la dirección en que lo hacían. Cada alumno respondió a un total de 60 presentaciones.

Contenidos

0. Cargar todos los datos (si tiene problemas con el paso 1 y 2)

Todos los datos de los experimentos están en un archivo de texto all.txt que se puede bajar de acá: http://www.df.uba.ar/users/gsolovey/fisica2/Matlab_Psicofisica/data/all.txt

Guarden ese archivo y para cargar los datos hagan en el Command Window

load all.txt

Ese archivo tiene 5 columnas.

1 - RT:    tiempos de respuesta (en segundos)
2 - co:    grado de coherencia
3 - resp:  respuesta del sujeto en cada experimento (0 izq - 1 der)
4 - dir:   dirección del movimiento coherente en cada experimento (0 izq - 1 der)
5 - corr:  1 si la respuesta fue correcta y 0 si fue incorrecta

Para comodidad le vamos a cambiar crear una variable por cada columna:

RT   = all(:,1); % toma la primera columna de |all| y se la asigna a la variable |RT|
co   = all(:,2);
resp = all(:,3);
dir  = all(:,4);
corr = all(:,5);

Ahora pasen al punto 3 directamente

1. Importar los datos de un sujeto

El resultado de cada experimento está guardado en un archivo de matlab .mat. Primero bajen todos estos archivos que están acá:

http://www.df.uba.ar/users/gsolovey/fisica2/Matlab_Psicofisica/data/

y guárdenlos en una carpeta llamada data. Si no quieren bajar todos de a uno pueden bajar el archivo all.tgz a la carpeta de destino y descomprimirlo desde una terminal de linux (desde windows debería servir cualquier programa descoprimir), así:

$> tar -xzvf all.tgz

Ahora pueden importar Pueden importar cada uno de ellos usando load. Por ejemplo:

load Guille_2008_09_09_13_18_11.mat

Una vez que se importó la información contenida en el .mat la podemos visualizar en el Workspace. De hecho, se creó una "estructura" que se llama experimento. Una estructura es un conjunto de variables agrupadas. Pueden acceder al contenido de la estructura haciendo doble-click en el Workspace o bien desde el Command Window. Usando esto último

experimento

% Se muestra una salida como esta:
%
% experimento =
%            RT: [22.0070 2.4219 3.3344 8.4595 1.6191]
%          resp: [0 1 1 0 1]
%     coherence: [1x60 double]
%           dir: [1x60 double]
%
% Esto quiere decir que la estructura |experimento| tiene cuatro variables
% dentro: |RT|, |resp|, |coherence| y |dir| que tienen lo siguiente:
%
%  RT:           tiempos de respuesta (en segundos)
%  resp:         respuesta del sujeto en cada experimento (0 izq - 1 der)
%  coherence:    grado de coherencia
%  dir:          dirección del movimiento coherente en cada experimento (0 izq - 1 der)

% y son 60 elementos porque se hicieron 60 presentaciones del estímulo.
%
%

% a) Grafiquen el tiempo de respuesta y la coherencia. Busquen (al menos a ojo)
% alguna correlación entre
% eventos con tiempos de respuesta largos y valores de coherencia chicos (y
% viceversa.

experimento = 

           RT: [1x60 double]
         resp: [1x60 double]
    coherence: [1x60 double]
          dir: [1x60 double]

2. Importar los datos de todos los sujetos

Para importar todos los datos de los sujetos usamos el siguiente código (está comentado, pero si no se entiende, pregunten!)

clear all
close all

A=what;  %guarda en |A| una lista de los archivos de matlab del directorio en el que se está trabajando.
d=A.mat; %se queda con los que son |.mat| que son los que nos interesan

RT=[];resp=[];dir=[];co=[];suj=[];  %crea estas variables (en principio vacías)

for i=1:size(d)  % hace un loop que corre sobre todos los elementos de |d|
    load(d{i});  % carga los datos del sujeto |i|
    L=length(experimento.resp); % numero de presentaciones del estímulo que el sujeto respondió

    resp=[resp;experimento.resp']; % acumula en |resp| las respuestas que dio el sujeto
    temp=experimento.RT'; RT=[RT;temp(1:L)]; % acumula en |RT| los tiempos de rta. del sujeto
    temp=experimento.dir'; dir=[dir;temp(1:L)]; % acumula en |dir| la dirección que tenían las partículas coherentes
    temp=experimento.coherence'; co=[co;temp(1:L)]; % guarda la coherencia usada en cada presentación
end
dir = dir > 0.5; % para poner la direccin en 0 y 1, igual que la respuesta.
corr=dir==resp;  % las respuestas correctas
COS=unique(co);  % Los valores de coherencia

Descripción del contenido de las variables

RT:    tiempos de respuesta (en segundos)
co:    grado de coherencia
resp:  respuesta del sujeto en cada experimento (0 izq - 1 der)
dir:   dirección del movimiento coherente en cada experimento (0 izq - 1 der)
corr:  1 si la respuesta fue correcta y 0 si fue incorrecta
COS:   Los valores de coherencia que usamos en el experimento

3. Tiempos de respuesta

a) Hacer un histograma de los tiempos de respuesta.

Seguramente se encontraron con tiempos de respuesta 'muy largos' que se pueden atribuir a errores experimentales. Piensen cuál sería el rango típico de tiempos de respuesta y hagan el histograma restringiendo los tiempos de respuesta a ese rango. Para eso es útil usar la función find.

La función find se puede usar para buscar los elementos de un vector que cumplen con cierta condición. La función find devuelve un vector que es una lista de los índices en los que se cumple la condición deseada. Por ejemplo:

a   = [2 13 -4 -7 12 -123]; %crea un vector de 6 componentes
find( a>0 )  %devuelve los índices (ubicaciones) de los elementos de |a| que son positivos.
find( a>10 & a<20 ) %devuelve los índices en los que |a| es mayor que 10 y menor que 20

ans =

     1     2     5


ans =

     2     5

En este caso usamos find para hacer un histograma únicamente con los tiempos de respuesta que son menores que 1 seg.

figure
hist( RT( find(RT<5) ) )    %% hace un histograma de 10 bines (default)
xlabel('Tiempo (seg)');
ylabel('# casos');

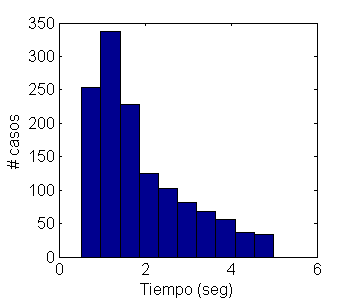
b) Encuentren un rango típico de RT y hagan el histograma en esa región (usando la idea del código anterior).

c) Encuentren qué fracción de los datos están descartando. (se puede usar la función length: length(v) devuelve el número de elementos de v.

d) Tiempos medios de respuesta en función de la coherencia. ¿Cómo esperaría que resulte esta función: creciente, constante o decreciente? Esto se puede analizar también usando la función find de la siguiente forma. Fíjense que esta vez se usa el find para restringir los valores sobre los que se hace el promedio a aquellos que tienen un valor de coherencia dado por COS(i) y tiempo de respuesta menor que 5 seg.

for i=1:length(COS);
    RTm(i) = mean( RT( find( co==COS(i) & RT < 5) ) );
    CORRm(i) = mean( corr( find( co==COS(i) & RT < 5) ) );
end

figure
plot(COS, RTm, 'o-')
xlabel('grado de coherencia');
ylabel('tiempo de respuesta medio');

hold on
plot(COS, CORRm,'ro-')

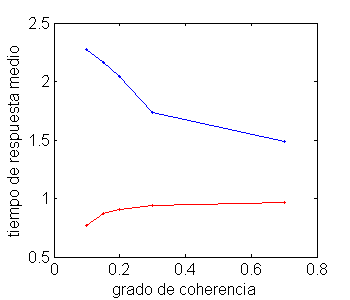
4. Porcentaje de respuestas correctas

Usando un código análogo al de 2.d) calcule y grafique el porcentaje de respuestas correctas en función de la coherencia.

5. Media vs Mediana

Repetir el ejercicio 2.d) y el 3 calculando la mediana en lugar de la media. Analizar las ventajas que tiene uno frente al otro. ¿Es necesario cortar las distribuciones descartando tiempos largos si usan la mediana?

6. ¿Y los random walks?

¿Qué relación tiene este experimento con el ejercicio 6) de la guía computacional de random walks?

http://www.df.uba.ar/users/gsolovey/fisica2/Matlab_RW/random_walk.html

-------------------------------------------------------- http://www.df.uba.ar/users/gsolovey/fisica2/fisica2.html

Published with MATLAB® 7.3