Movimiento Browniano - Caminata al azar

Práctica de Física 2 (biólogos y geólogos) - Sigman returns - 2o cuatrimestre de 2008 http://www.df.uba.ar/users/gsolovey/fisica2/fisica2.html

Objetivo: En esta práctica vamos a simular una partícula haciendo una caminata al azar en una dimensión. La partícula se mueve una distancia 'dx' durante un tiempo 'dt' y luego cambia aleatoriamente de dirección (+dx o con probabilidad p y -dx con probabilidad (1-p)). Discretizamos el tiempo en unidades de 'dt', de modo que:

y por lo tanto la posición de la partícula en cada instante de tiempo viene dada por:

Contenidos

clear all %borramos todas las variables
close all %cerramos todos las figuras

1. Generar números al azar

Como el movimietno de la partícula es aleatorio, necesitamos sortear la dirección de la partícula en cada paso de tiempo (cada 'dt'). Para eso vamos a usar un generador de números al azar* que tiene Matlab (y en general todo lenguaje de programación).

*: En realidad, lo que se generan son números pseudo-aleatorios, que aparentan no tener ningún patrón pero están construidos por algoritmos que los generan en cadena.

a) La función rand genera números al azar entre 0 y 1 con una distribución uniforme. ¿Qué quiere decir esto?

b) Cada vez que se ejecuta, se genera un número al azar diferente. Probarlo!

rand

ans =

    0.5221

Si se quieren generar varios números juntos, se puede hacer así:

rand(1,5); %genera un vector fila de 5 números al azar

2. Guardar N números al azar entre 0 y 1 y hacer un histograma con los resultados.

N=100; % cantidad de números aleatorios que vamos a generar
datos=rand(N,1); % se generan los números y se guardan en la variable |datos|
figure
hist(datos, 10) %10 es el número de bines del histograma

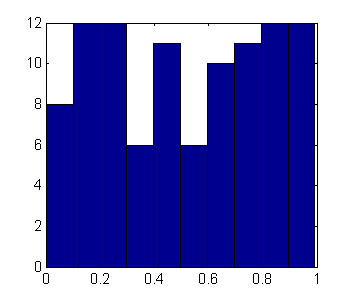
a) ¿Qué representa la altura de cada barra del histograma? ¿Por qué, si los números se sortean con una distribución uniforme, el histograma se ve tan irregular?

b) ¿Qué intervalo representa el ancho de cada barra? Si tiene dudas, busque en la ayuda de Matlab la función hist.

c) Ver que con valores más grande de N, el histograma representa cada vez mejor la distribución de probabilidad. Ver también qué sucede si se usan bines más pequeños.

d) ¿Cómo haría para generar números al azar entre 0 y 15? ¿y entre -1 y 2? Hacerlo y construir nuevos histogramas. Ayuda: Utilice la misma función rand y expanda el resultado apropiadamente. Si es necesario, vea uno de los ejemplos de la Ayuda de Matlab para la función rand

3. Generar un número al azar binario {-1,1} con igual probabilidad.

Es decir, definir una variable aleatoria 's' que valga 1 o -1 con igual probabilidad. Ayuda: Use la estructura if para lograr lo siguiente: 

x = número aleatorio entre 0 y 1.
si x es menor que 0.5
   asignar a s el número -1
caso contrario
   asignar a s el número 1

4. Generar un número al azar binario {-1,1} con probabilidad p de ser -1 y y (1-p) de ser 1.

¡Nos vamos acercando a lo que necesitamos para la caminata al azar!

5. Una caminata aleatoria

Guarde en el vector x la posición de la partícula como función del tiempo. Para esto defina la posición inicial, por ejemplo x(1)=0. Luego genere un loop que recorra el tiempo (usando una nueva variable, i=1:1000, por ejemplo si se van a simular T pasos de tiempo). Use el siguiente código y modifíquelo si es necesario. 

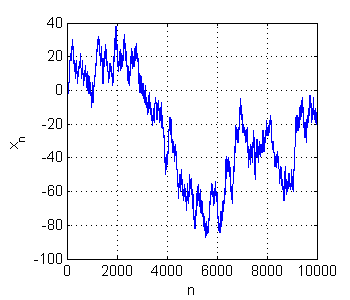
clear x

p=0.5;
deltax=1;
T=10000;

x(1)=0;
for i=2:T
    if (rand < p)
        x(i)=x(i-1)+deltax;
    else
        x(i)=x(i-1)-deltax;
    end
end

plot(1:T,x)
grid on
xlabel('n');
ylabel('x_n');

5. 100 caminatas aleatorias

Ahora vamos a generar 100 caminatas aleatorias, todas partiendo desde el mismo punto. Vamos a guardar el recorrido en una matriz x que tendrá 100 columnas, donde cada una de ellas tendrá la posición de cada partícula en el tiempo. Vea el siguiente código y esté seguro de que lo entiende. 

clear x

p=0.5;
deltax=1;
T=1000;

for part=1:100
    x(1,part)=0;
    for i=2:T
        if (rand < p)
            x(i,part)=x(i-1,part)+deltax;
        else
            x(i,part)=x(i-1,part)-deltax;
        end
    end
end

plot(1:T,x)
xlabel('tiempo');
ylabel('posición');

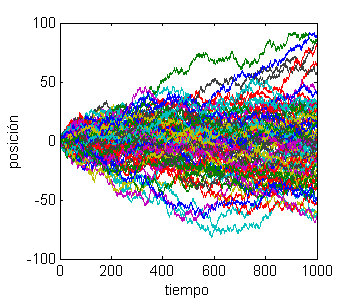
a) Calcule el valor medio de la caminata y comparar con el resultado esperado. ¿Por qué difieren? ¿Qué sucede si se aumenta el número de partículas?

Ayuda: Como x es una matriz, la función mean promedia cada columna por separado y arma un vector que tiene el promedio de cada columna. Si se fijan, hemos guardado el recorrido de cada partícula en una columna diferente. Por eso, para calcular el promedio sobre todos las partículas, a un tiempo fijo, tenemos que trasponer la matriz, es decir, calcular mean(x'). 

plot(1:T,mean(x'))
xlabel('n');
ylabel('<x>');

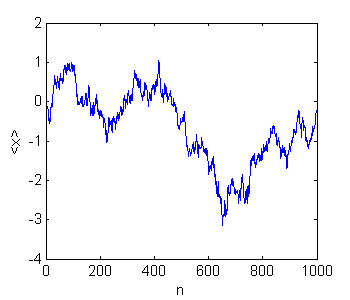
Si le resulta extraña la forma de calcular el promedio, a lo mejor este código le resulte más familiar para calcular el promedio de la posición en función del tiempo. 

for i=1:T
    posicio_media(i) = mean( x(i,:) ); % esto calcula el promedio de la posición
                                       % para el tiempo |i| y entre todas las
                                       % partículas (de ahi el ":" que indica
                                       % que se calcula sobre todas las
                                       % columnas de |x|.
end

Una forma de cuantificar la dispersión de las partículas es calculando la varianza, esto es la distancia cuadrática de los puntos respecto del valor medio. 

plot(1:T,mean(x'.^2)-mean(x').^2)
xlabel('n');
ylabel('<x^2> - <x>^2');

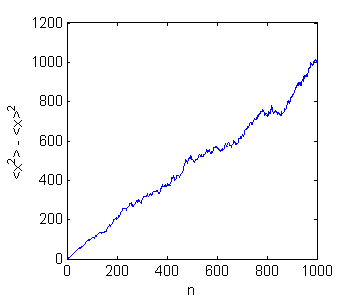
a) Ajusten la posición cuadrática media con una recta usando la función Tools + Basic Fitting dentro de la ventana de la Figura. Si ve que la función tiene una tendencia y luego cambia, use sólo la región que tiene una tendencia marcada.

b) ¿Qué relación encontraron entre la varianza y el tiempo (medido en unidades de pasos) para una caminata aleatoria?

6. Tiempos de llegada

Usando el código anterior, reformúlelo para calcular lo siguiente. Suponga que la partícula que hace la caminata aleatoria se puede mover libremente hasta que llega a una distancia L=10 o L=-10 del origen. Esos dos puntos son fijos (de absorción). El objetivo del problema es calcular para cada partícula el tiempo que tarda en llegar a L=10 y L=-10. Piense cómo hacerlo y luego pregunte si no le sale.

Sugerencia: Una opción es cambiar el loop for i=2:T por un nuevo loop que se while (abs(x(i,part))<L). Otra opción es usar la instrucción break para salir del loop una vez que la partícula llegó a la posición correspondiente.

Luego construya un histograma con los resultados de los tiempos medidos.

-------------------------------------------------------- http://www.df.uba.ar/users/gsolovey/fisica2/fisica2.html


Published with MATLAB® 7.4