Transformación Fourier de la Función Gaussiana

Cómo dibujar una onda armónica

 En esta primer parte veremos un ejemplo de có se puede visualizar el avance de una onda armónica en el tiempo. Para ello, modificaremos levemente el programa sin3.f que vimos en la práctica anterior, agregándole la variable temporal. El programa se llama armonic.f y es el siguiente: 

	program armonic

c....... This program prints two columns in files "wavet###.dat"
c	 where ### means different times.
c	X: "npoints" angles between 0 and 6*Pi
c	Y: sin(kX-wT)


c....... variables declaration
	implicit real*8(a-h,o-z)

        common/blockwave/rk,w
	data npoints,ntpoints/2000,10/	!! npoints: points in x
c					!! ntpoints: number of graphs in t

c....... calculation of Pi
	Pi = 2.0d0*dasin(1.0d0)

c....... calculation of angular step
	dang = 6.0d0*Pi/npoints	

c...... initialization
	rk = 1
	w = 1

	print*,' for the function y=sin(kX-wT) '
	print*,' give the value of k :'
	read*,rk
	print*,' give the value of w :'
	read*,w
	print*,' '

c...... calculation of T=Period
	period = 2.0d0*Pi/w
	deltat = Period/ntpoints
	t = -deltat

c...... loop in time ( 1 cycle)
	do 500 it=1,ntpoints

	  t = t + deltat

c.......  table generation for this particular time
	  x = -dang
	  do 100 i=1,npoints		!! loop in x
		x = x + dang
		y = wave(x,t)
		write(10+it,25) x,y
100	  continue			!! end loop in x
25	  format(5x,f10.3,3x,f14.4)	


500	continue		!! end loop in time

	stop
	end

c------------------------------------------------------------

	function wave(x,t)
	
	implicit real*8(a-h,o-z)
	common/blockwave/rk,w

	wave = sin(rk*x - w*t)

	return
	end

Este programa construye una serie de files (fort.11, fort.12, fort.13, ...) que podrán ser dibujados usando xmgrace. Una forma de visualizar fácilmente el avance temporal, es graficando los resultados de la siguiente forma:

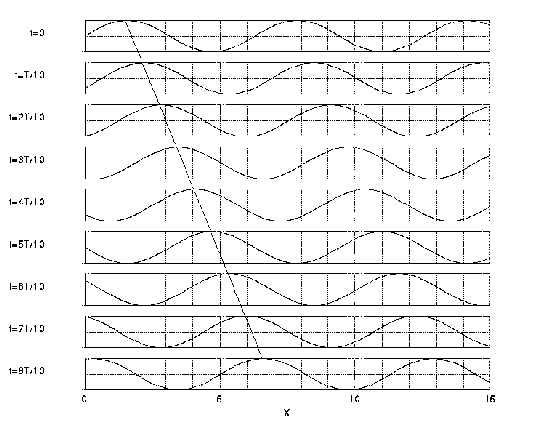
Mediante la pendiente podremos hallar la velocidad con que avanza la onda.

Ejercicios:

  • Modificar el programa y hallar las velocidades de avance de la onda (grupo o fase?) para distintos casos (considerar tambien velocidades negativas).
  • Qué pasa si en lugar de sin se pone cos?

    Construcción de un paquete de ondas

     Ahora modificaremos el programa anterior, y construiremos un paquete de ondas, con dos ondas sinusoidales, cuyas frecuencias no estan muy separadas. Esto se puede hacer modificando la función wave de la siguiente manera: 

    	function wave(x,t)
	
	implicit real*8(a-h,o-z)
	common/blockwave/rk,w

	deltak = 0.1
	deltaw = 0.1
	wave = sin((rk+deltak)*x - (w+deltaw)*t) +
     +         sin((rk-deltak)*x - (w-deltaw)*t)

	return
	end

    Si todo anda bien, deberán recibir resultados como el siguiente:

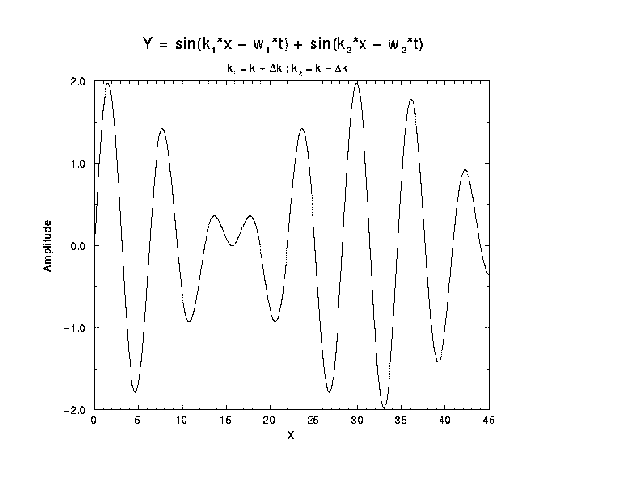
    Ejercicios:

  • Hallar las velocidades de avance de las componentes (grupo o fase?) y la velocidad de grupo del paquete.
  • Qué pasa si reemplazamos uno de los sin por un cos?
  • Modificar el programa y variar las amplitudes relativas, de modo que la amplitud de una componente sea mucho mayor que la otra.
  • Cómo harías una onda estacionaria? (hacélo).
  • Modificar el programa agregando mas ondas al paquete. (si querés poner muchas ondas, es preferible introducir un loop en la función wave).

    Conociendo la función Gaussiana

     Lo primero que vamos a hacer para conocer la función Gaussiana es dibujarla. Para ello, haremos uso del programa gaussian.for. Allí encontraremos la siguiente subrutina: 

            real*8 function gauss(i,apot,wpot,dx)
        implicit real*8(a-h,o-z)

c.......construct a Gaussian wavepacket function

        common/bckdat/pi
        data rzero,one,two/0.0d0,1.0d0,2.0d0/

        x = i*dx
        f1=one/dsqrt(wpot*dsqrt(pi))
        gauss= f1*exp(-(x-apot)**2/(two*wpot**2))

        return

    que producirá los valores del Gaussiano, para cada punto x=i*dx. Si todo está correcto, los resultados deberán aparecer en el directorio (si compilás y ejecutás !).

    Ejercicios:

  • Qué significa apot ?
  • Qué significa wpot ?
  • Variar estas variables y graficar los cambios
  • Integrar los resultados y comprobar la normalización

    Transformación Fourier

     Para familiarizarnos con la Transformación de Fourier, transformaremos una función simple 

    y(x)=sin(wt + phi)

    usando el programa fouriers.for.

    Si el programa es usado correctamente (en éste caso usamos npts=50, tau=1, w=0.2 y phi=0), deberán obtener resultados como en el siguiente ejemplo:

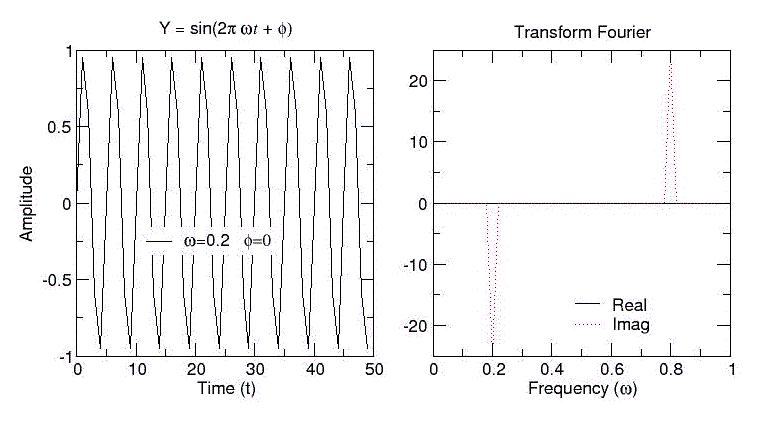
    Ejercicios:


  • Graficar los resultados para distintos valores de la frecuencia y la fase
  • Cambiar los números de puntos y graficar
  • Qué significa la parte real y la imaginaria?
  • Por qué hay dos picos en la transformada de la figura anterior?
  • Modificá el programa, transformando otras funciones.

    Paquete de Ondas Gaussianas

     Ahora construiremos un paquete de ondas Gaussiano, usando el programa wavepacket.for.

    Este paquete de ondas se construye multiplicando la función Gaussiana por una función Hankel.

    Ejercicios:

  • Qué significan las partes real e imaginaria?
  • Comprobar la variación de los resultados para diferentes energías
  • Integrar los resultados y comprobar la normalización
  • Cómo harías avanzar al paquete de ondas? Modificá el programa y probá

    Transformación Fourier del Paquete de Ondas Gaussianas

     Ahora haremos la Transformación Fourier del paquete de ondas Gaussiano, usando el programa invfourgauss.for.

    Ejercicios:

  • En la función transformada: Qué significan las partes real e imaginaria?
  • Comprobar la variación de los resultados para diferentes energías
  • Comprobar la variación de los resultados para diferentes valores de X0
  • Integrar los resultados y comprobar la normalización
  • Realizar la transformación en el programa modificado, (el que avanza el paquete de ondas en el tiempo).

    Lecturas Auxiliares Recomendadas:


  • Heisenberg's Uncertainty Principle Java Applet - by Mark Sutherland.