Problemas del Curso Física 4

Instructor: Darío Mitnik

Transformación Fourier de la Función Gaussiana

Conociendo la función Gaussiana

 Lo primero que vamos a hacer para conocer la función Gaussiana es dibujarla. Para ello, haremos uso del programa gaussian.for. Allí encontraremos la siguiente subrutina: 

        real*8 function gauss(i,apot,wpot,dx)
        implicit real*8(a-h,o-z)

c.......construct a Gaussian wavepacket function

        common/bckdat/pi
        data rzero,one,two/0.0d0,1.0d0,2.0d0/

        x = i*dx
        f1=one/dsqrt(wpot*dsqrt(pi))
        gauss= f1*exp(-(x-apot)**2/(two*wpot**2))

        return

que producira los valores del Gaussiano, para cada punto x=i*dx. Si todo está correcto, los resultados deberán aparecer en el directorio (si compilás y ejecutás !).

Preguntas:

  • Qué significa apot ?
  • Qué significa wpot ?
  • Variar estas variables y graficar los cambios
  • Integrar los resultados y comprobar la normalización

    Transformación Fourier

     Para familiarizarnos con la Transformación de Fourier, transformaremos una función simple 

    y(x)=sin(wt * phi)

    usando el programa fouriers.for.

    Si el programa es usado correctamente (en éste caso usamos npts=50, tau=1, w=0.2 y phi=0), deberán obtener resultados como en el siguiente ejemplo:

    Preguntas:

  • Graficar los resultados para distintos valores de la frecuencia y la fase
  • Cambiar los números de puntos y graficar
  • Qué significa la parte real y la imaginaria?
  • Por qué hay dos picos en la transformada de la figura anterior?
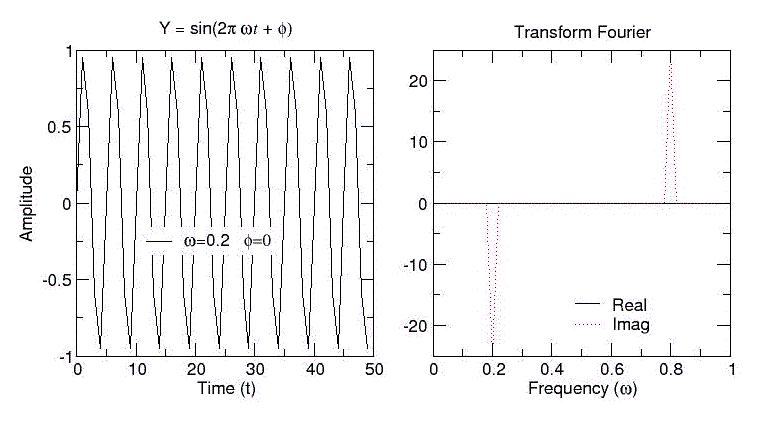
  • Modificá el programa, transformando otras funciones.

    Paquete de Ondas Gaussianas

     Ahora construiremos un paquete de ondas Gaussiano, usando el programa wavepacket.for.

    Este paquete de ondas se construye multiplicando la función Gaussiana por una función Hankel.

    Preguntas:

  • Qué significan las partes real e imaginaria?
  • Comprobar la variación de los resultados para diferentes energías
  • Integrar los resultados y comprobar la normalización
  • Cómo harías avanzar al paquete de ondas? Modificá el programa y probá

    Transformación Fourier del Paquete de Ondas Gaussianas

     Ahora haremos la Transformación Fourier del paquete de ondas Gaussiano, usando el programa invfourgauss.for.

    Preguntas:

  • En la función transformada: Qué significan las partes real e imaginaria?
  • Comprobar la variación de los resultados para diferentes energís
  • Comprobar la variación de los resultados para diferentes valores de X0
  • Integrar los resultados y comprobar la normalización
  • Realizar la transformación en el programa modificado, (el que avanza el paquete de ondas en el tiempo).

    Lecturas Auxiliares Recomendadas:


  • Heisenberg's Uncertainty Principle Java Applet - by Mark Sutherland.