- Demostrar que el término de corrección relativista a
la energía cinética es
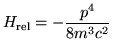
- Demostrar que en primer orden de teoría de perturbaciones,
la corrección a la energía en los iones hidrogenoides es
![$\displaystyle \Delta_{\mathrm rel} = -\frac{1}{2 m c^2}
\left[
E_n^2 + 2 E_n
(\...
...rac{Z e^2}{4 \pi \epsilon_0})^2
{\langle \frac{1}{r^2} \rangle}_{nlm_l}
\right]$](img3.png)
- Demostrar que la corrección anterior es igual a
![$\displaystyle \Delta_{\mathrm rel} = -E_n \frac{(Z \alpha)^2}{n^2}
\left[
\frac{3}{4} - \frac{n}{l + 1/2}
\right]$](img4.png)
- Comparar las correcciones relativistas (relativas y absolutas)
en los estados
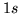 y
y 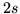 y
y 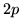 del hidrógeno,
junto con las
del hidrógeno,
junto con las 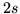 del C
del C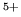 y la
y la 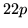 del U
del U .
A partir de qué ion se debe tener en cuenta esta corrección
para tener los valores de energías aceptables en un 0.5%?
.
A partir de qué ion se debe tener en cuenta esta corrección
para tener los valores de energías aceptables en un 0.5%?
El término de corrección spin-órbita se escribe
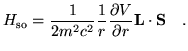 |
- Calcular
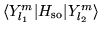 para
para 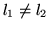 .
.
- Expresando
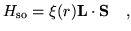
calcular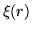 para el potencial Coulombiano.
para el potencial Coulombiano.
- Demostrar que el valor de la corrección spin-órbita en primer
orden de teoría de perturbación es
![$\displaystyle \Delta_{\mathrm so} = \frac{\hbar^2}{2} \langle \xi(r) \rangle
\left[
j(j+1) - l(l+1) - \frac{3}{4}
\right]$](img16.png)
- Tomando en cuenta que el valor medio
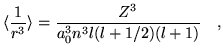
calcular el valor de la corrección para los casos generales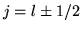 .
.
- Calcular la corrección spin-órbita para los casos pedidos
en el punto (1d).
El término de Darwin se escribe
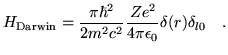 |
- Expresar la corrección de Darwin en forma general, para
los diferentes números cuánticos
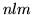 .
.
- Expresar la corrección total, dada por la suma de los términos
relativistas, spin-órbita y Darwin.
- Obtener las energías, correctas a primer orden perturbativo,
de los estados señalados en el punto (1d).
- Comparar la expresión de la energía con el resultado
exacto que se obtiene resolviendo la ecuación de Dirac
![$\displaystyle E_{nj} = mc^2
\left\{
\left[
1 +
\left(
\frac{Z \alpha}
{n - j - 1/2 + [(j+1/2)^2 - Z^2 \alpha^2]^{1/2} }
\right)^2
\right]^{-1/2}
-1
\right\} ~~~.$](img21.png)
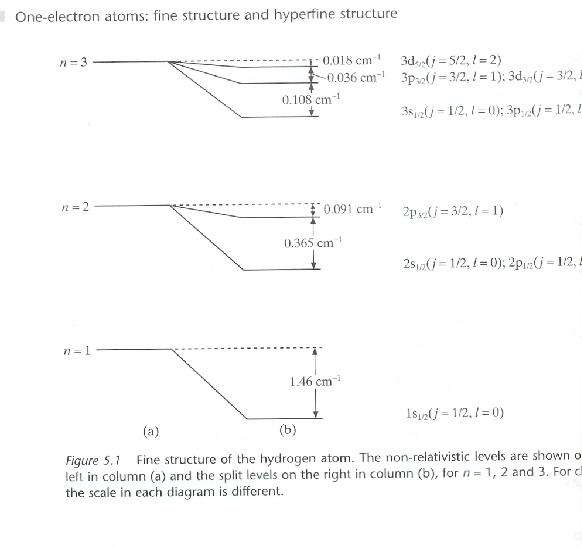
- Utilizando los resultados anteriores, comprobar que
el espectro del átomo de hidrógeno coincide con los dados
en las Figuras 1 y 2