CV
- Nacido en Pergamino, Buenos Aires, Argentina, el 15
de Junio de 1955.
- Nacionalidad: Argentina.
CI 7.066.619 Policía Federal.
- Profesor Asociado (dedicación exclusiva), Departamento
de Física, Facultad de Ciencias Exactas y Naturales,
Universidad de Buenos Aires (Junio de 1993 - presente), ocupa el
cargo en forma regular desde 1995.
- Miembro de la Carrera del Investigador Científico,
Consejo Nacional de Investigaciones Científicas y
Técnicas de Argentina (CONICET) (Enero 1991 - presente)
Categoría: Investigador Principal (a partir de Junio de 2004).
Categoría sistema de incentivos: I (última confirmación 2009)
- Doctor en Ciencias Físicas. Universidad de
Buenos Aires. Agosto de 1984.
- Licenciado en Ciencias Físicas.
Universidad de Buenos Aires. Noviembre de 1978.
- *
- Dinámica de los lasers
- *
- Turbulencia y desordenes espacio-temporales,
transición a la turbulencia.
- *
- Formación de estructuras espaciales. Ecuaciones no
lineales (en derivadas parciales) de sistemas extensos.
- *
- Sistemas dinámicos, teoría ergódica y mecánica
estadística.
- *
- Teoría de grupos.
- *
- Física no-lineal y sus aplicaciones.
- *
- Dinámica no lineal, caos en pocas dimensiones y sus
aplicaciones.
- *
- Teoría de bifurcaciones y sus aplicaciones.
- *
- Dinámica estocástica y procesos estocásticos.
- *
- Dinámica de poblaciones.
- *
- Biología teórica y modelos biomatemáticos.
- *
- Modelos para Aedes aegypti y enfermedades transmitidas por
el mosquito.
- *
- Epistemología y Ense
'Ananza de la Ciencia.
- *
- Hidrodinámica, flujos en canales abiertos y
aplicaciones al dise
Ánno de obras hidráulicas.
- *
- Física nuclear y física de muchos cuerpos.
Aproximaciones semiclásicas. Modelos algebraicos (IBM) de
los niveles nucleares de baja energía.
- -
- Becario de iniciación del CONICET. (1981-1982). Tema:
Procesos de relajación en sistemas finitos y su
límite termodinámico.
- -
- Becario de Perfeccionamiento del CONICET. (1983-1985).
Tema: Estudios macroscópicos de la dinámica de muchos
cuerpos.
- -
- Becario externo del CONICET. (1985-1987). Tema:
Teoría de grupos y física de muchos cuerpos. Lugar
de trabajo: Drexel University, Philadelphia, U.S.A. .
- -
- Beca del ICTP-Trieste para participar de ``School on
Dynamical Systems'' (9-27 de septiembre de 1991).
- -
- Beca de alto nivel. Ministere de la Recherche et la Technologie de
Francia, 1993. Lugar de trabajo: Laboratorio No-Lineal de Niza.
- -
- Distinguido como Outstanding Referee por la American Physical
Society dentro de los primeros 534 científicos merecedores de esta distinción
en Marzo de 2008.
http://www.aps.org/publications/apsnews/200803/referees.cfm
- -
- El desarrollo de los modelos de Dengue fue elejido como uno de los tres
avances científicos del a
'Annno 2009 por el programa periodístico: Científicos
Industria Argentina dirigido por el Dr. Adrián Paenza.
- -
- Reviewer para las publicaciones de la American Physical
Society: Physical Review - Physical Review Letters - Journal of
Mathematical Physics. (1987- )
- -
- Reviewer para Optics Communications. (Esporadicamente)
- -
- Reviewer para Physica D. (1998-2003)
- -
- Reviewer para Medical Science Monitor. (2006-)
- -
- Reviewer para Mathematical Reviews. (2007- )
- -
- Reviewer para Ecological Modelling (2008-).
- -
- Reviewer para European Journal of Physics D (2008-)
- -
- Reviewer para Journal of Mathematical Analysis and Applications (2009-)
- -
- Reviewer para Journal of Mathematical Biology (2010-)
- -
- Reviewer para BioMed Central (2010-)
- -
- Reviewer para Journal of Theoretical Biology (2010-)
- -
- Miembro de la Comisión Técnica Asesora de Física, Matemática
y Química de la Universidad de Buenos Aires, Noviembre de 1996 - Marzo
de 1998.
- -
- Miembro del Consejo Directivo de la Facultad de Ciencias Exactas y
Naturales de la Universidad de Buenos Aires. 1998 - 2001 (tomó Licencia
por razones de salud en marzo de 2000).
- -
- Jurado del Concurso de Becas para Estudiantes Destacados en
Ciencias y Humanidades, Fundación Antorchas 1992.
- -
- Jurado del Concurso de Colaboración con Investigadores
Extranjeros (Argentina-Brasil-Chile) de la Fundación Antorchas, 1999.
- -
- Evaluador para CONICET, UNSAM, UNR, ANCPyT, ...
- -
- Jurado de tesis de doctorado:
- *
- Elia Eschenazi. Drexel University, 1989.
- *
- James Heagy. Drexel University, 1990.
- *
- Francisco E. A. Parisi. Universidad de Buenos Aires, 1994.
- *
- María José Sanchez. Universidad de Buenos Aires, 1994.
- *
- Rafael González. Universidad de Buenos Aires, 1995.
- *
- Raúl Oscar Vallejos. Universidad de Buenos Aires, 1995.
- *
- Guillermo Ortega. Universidad de Buenos Aires, 1996.
- *
- Sergio Pablo Ferro. Universidad de Buenos Aires, 1998.
- *
- Pablo Balenzuela. Universidad de Buenos Aires, 2002.
- *
- Laura Sanchez. Universidad de Buenos Aires, 2003.
- *
- Alejandro Rosenfeld. Universidad de La Plata, 2003.
- *
- María Florencia Carusela, Universidad de Buenos Aires, 2006.
- *
- Ana Cecilia Tablar, Universidad Nacional del Sur (Matemáticas), 2007.
- *
- Luis Angel Martino,Universidad de Buenos Aires, 2009.
- *
- Leonardo A Saravia, Universidad de Buenos Aires (Biología), 2010.
- *
- Marcos Andres Madrid. Universidad de La Plata (Física), 2013.
- *
- Irene Duarte Gandica, Universidad de General Sarmiento (matemática), 2013.
- -
- Jurado de auxiliares docentes en el CEFIEC-FCEN-UBA. 2005, 2010.
- -
- Jurado de concurso de profesores en la Universidad de General Sarmiento,
2009.
- -
- Organizó el primer workshop regional e interdisciplinario de
dinámica no-lineal ``Buenos Aires Dinámico'' junto la Dra.
Lilia Romanelli. Diciembre 3 y 4 de 1992. Participantes de física,
química, matemática, economía, meteorología,
biología y otras ramas de las ciencias.
- -
- Miembro del Comité Organizador del Workshop Internacional
MEDYFINOL-1993 realizada en Mar del Plata, agosto de 1993.
- -
- Organizador con Cristina Masoller del ``FIRST `RIO DE LA PLATA'
WORKSHOP ON NOISE, CHAOS, AND COMPLEXITY IN LASERS AND NONLINEAR
OPTICS'', Colonia del Sacramento, Uruguay, 1 - 5 December, 2003
- -
- Subsidio anual del CONICET (PIA). Tema: Dinámica de sistemas
extendidos espacialmente, 1992.
- -
- Subsidio de Investigación de la Universidad de Buenos
Aires (X86?). Tema: Dinámica No Lineal. Período cubierto 4/92 -
3/94. Destino: gastos normales de Investigación. $5850
- -
- Subsidio para Investigadores Jóvenes. Fundación
Antorchas. Período cubierto 4/92 - 3/93. Tema: Dinámica No
Lineal. Destino: Equipamiento. Monto $4000.
- -
- Subsidio para viaje. Fundación Antorchas, 1993. Monto $800.
- -
- Subsidio de la CEE. Tema: Estructuras Espacio Temporales en Lasers.
Colaboración con: J. Tredicce (INL-Niza), T. Arecchi (Florencia, Italia),
A. Hnilo (CITEFA, Argentina). Monto $60000.
- -
- Subsidio para Investigadores Jóvenes. Fundación
Antorchas. Período cubierto 4/95 - 3/96. Tema: Dinámica No
Lineal. Destino: Equipamiento. Monto $4000.
- -
- Subsidio de Investigación de la Universidad de Buenos
Aires (Ex162). Tema: Dinámica No Lineal. Período cubierto 4/95 -
3/97. Destino: gastos normales de Investigación.
- -
- Subsidio Antorchas para colaboración internacional con el Dr. Mario
A. Natiello, KTH, Estocolmo, Suecia. El Departamento de Matemática del
KTH recibió un subsidio STINT (Suecia) para colaborar con el IMPA (Brasil)
y nuestro grupo de investigación. Este subsidio obra de contraparte.
- -
- Subsidio UBA (Tw04). Dinámica No-lineal Aplicada. Período cubierto
1998-2000, monto $7000.
- -
- Participa como investigador en el Proyecto 6-5030 del
FONCYT titulado ''Estudio sobre la nanoestructura y dinámica de
superficies" (director Roberto Salvarezza, INIFTA), Período
cubierto 2001-2003.
- -
- Subsidio UBA programación 2004-2006. Proyecto X308, Dinámica de
sistemas complejos (X308). Director.
- -
- Subsidio en Red, proyecto PICTR2002-00087, período cubierto
2005-2007, Eco-epidemiología matemática: aplicaciones a la propagación
del Dengue y el Hantavirus. Director.
- -
- Subsidio CONICET, PIP 5969, 2005-2006, Dinámica y termodinámica de
sistemas finitos relacionados. Director C.O. Dorso. Co-director, H.G. Solari.
- -
- Subsidio UBA, X210 (2008-2011). Sistemas complejos. Director H. G.
Solari, Co-director: Nicolás Schweigmann. Monto $60000.
- -
- Subsidio UBA, 20020100100734 (2011-2014). Biología y modelos bio-matemáticos de Aedes aegypti. Director H. G. Solari, Co-director: Nicolás Schweigmann.
- -
- Subsidio UBA,20020130100361BA, Modelado de la dinámica espacio-temporal
del ``Achaparramiento del Maíz'' y su vector Dalbulus maidis.
- -
- Control de experimentos, adquisición de datos y
procesamiento estadístico en forma simultánea con
equipo PDP-11/45 (Laboratorio de Hidráulica Aplicada,
INCyTH, 1978).
- -
- Modelación numérica de fluidos (LHA-INCyTH, 1978-1979)
- -
- Cálculos de blindaje de radiación gamma.
(Laboratorio de Procesos
Radioquímicos, CNEA, 1979).
- *
- Ayudante de cátedra en el Departamento de Física
de la la Facultad de Ciencias Exactas y Naturales - UBA de
acuerdo al siguiente detalle:
- -
- Ayudante de segunda. Octubre 1977 a Junio de 1979.
- -
- Ayudante de primera. Julio de 1979 a Marzo de 1981 y
Agosto de 1981 a Abril 1984.
- -
- Jefe de Trabajos Prácticos. Mayo de 1984 a Agosto de
1985.
- *
- Profesor Visitante, Department of Physics and
Atmospheric Science, Drexel University, Septiembre 1987 a
Agosto de 1990.
- *
- Profesor Adjunto, Departamento de
Física, Facultad de Ciencias Exactas y Naturales,
Universidad de Buenos Aires, Octubre de 1990 a Mayo de 1993.
- *
- Profesor Asociado, Junio de 1993 a la fecha.
Algunas de las materias dictadas
- -
- Física 1 (Físicos)
- -
- Física I (Biólogos y Geólogos)
- -
- Física II (Químicos)
- -
- Física II (Biólogos y Geólogos).
- -
- Mecánica clásica
- -
- Mecánica quántica
- -
- Física Contemporanea II (profesorado)
- -
- Fisica Contemporanea I (profesorado)
En 2004 dicté por primera vez Física II (Biólogos y geólogos) dando
inicio a un acercamiento entre los departamentos involucrados para actualizar
estas materias cuyos programas eran (son?) copias del programa de física 2 de
los a
Ánnnnos 70. Los cambios que introduje en el programa en uso de la libertad de
cátedra se orientan a reemplazar temas de optica por temas de ondas y sus
aplicaciones en biología y geología, la parte de termodinámica fue ampliada
saliendose del temario básico (ingenieril) de las máquinas térmicas para
introducir termodinámica de las mézclas (relevante tanto a biología como a
geología) como termodinámica de las reacciones químicas, estas últimas
esenciales a la biología molecular de nuestros días.
En 2006 se me comisionó el dictado de Física Contemporanea II. La materia
no había sido dictada por dos a
'Annnnnos, y en a
'Annnnnos anteriores se habían usado
materias sustitutas y hasta una peregrinación por tres materias en un
cuatrimestre. La materia carecía de programa. En discusiones con la Dra Dibar
(CEFIEC) y en consulta con el Dr. Contreras (responsables del curriculum
inicial del profesorado en física) fuimos dando forma a la materia, que no está
organizada por contenidos (ya que no tiene un contenido específico), sino como
un taller de toma de conocimiento de la actualidad en la investigación en
física usando como disparador artículos de temas variados aparecidos en
Physics Today en los últimos a
Ánnnnnnos. Desde la física de partículas elementales
hasta los problemas éticos de la física actual, pasando por los lasers, los
motores brownianos, la turbulencia y la física de maremotos y terremotos, y
otros temas.
- -
- Temas de física matemática I: Teoría de
Grupos, 1985 -FCEN-UBA, en colaboración con Mario A.
Natiello.
- -
- Seminar on Non Linear Dynamics, 1988 and 1990. - Dept.
of Physics and Atmospheric Science, Drexel University.
- -
- Dinámica No-lineal, Departamento de Física,
FCEN - UBA, 1991, 1992, 1993, 1994, 1996 y 2002. El curso de 1991
fue la primera vez que se ense
'Annnnnnnó este tema en el Departamento de Física.
- -
- Teoría de grupos. Depto. de Física, FCEN - UBA, 1992, 1994 y 1996.
- -
- Sistemas complejos, 2005, 2007 y 2012 Este curso
ha sido dado solo por mi en el Departamento de Física.
- -
- Rebeca Falcione. Septiembre 2010-
- -
- Co-director de tesis de Licenciatura de (Lic.) Dora
Jezek, Tema: Dinámica variacional en sistemas de muchos
fermiones en modelos resolubles. Departamento de Física,
FCEN-UBA, 1985. (Investigadora del CONICET)
- -
- Director de tesis de licenciatura de Martín
Zimmermann, Departamento de Física, FCEN-UBA, 1991 - julio 1993.
- -
- Director de tesis de licenciatura de Mariano Vázquez.
Departamento de Física, FCEN-UBA, 1991 - mayo de 1993. (Mariano
Vázquez continuó estudios de doctorado en el Instituto Politécnico
de Barcelona.)
- -
- Director de la tesis de licenciatura de Guillermo Bustamante,
Departamento de Física, FCEN-UBA, 1993 - septiembre de 1995.
(Continuó con una pasantía en el IAFE.)
- -
- Director de la tesis de licenciatura de Diego Francisco
Departamento de Física, FCEN-UBA, 2001 - septiembre de 2002
- -
- Director de la tesis de licenciatura de Victoria Romeo Aznar
Departamento de Física, FCEN-UBA, 2009, Marzo de 2010.
- -
- Co-director de los estudios de doctorado de Gabriel B. Mindlin. (Ph.D.)
Topological Analysis of Chaotic Data. Department of Physics and Atm. Sc.,
Drexel University 1988-1991 (ver publicaciones 17-22). (Continuó con una beca
postdoctoral en la Universidad de Pamplona.)
- -
- Consultor en las tesis de doctorado de (ver publicaciones 14.,
17. y 22.): Elia Eschenazi (Director: R. Gilmore, Drexel University);
Nicholas Tufilaro (Director: A. M. Albano - Bryn Mawr University);
Francesco Papoff (Director: E. Arimondo, Universidad de Pisa); Martín
Zimmermann (Director M. A. Natiello - Uppsala University).
- -
- Director de la tesis de doctorado del Lic. Juan Aparicio,
Departamento de Física, FCEN - UBA (Nov. 1993 - Nov. 1999).
Título: Dinámica de Procesos Epidémicos Calificación:
Sobresaliente. (J. P. Aparicio continuó como postdoctorado en
Cornell University.)
- -
- Supervisor de PostDoctorado de Andrew Kent (Ph. D.), Abril
1994- Marzo 1995. Becario de la Royal Society - CEE.
- -
- Director de la tesis de doctorado del Lic. Alejandro Duarte. Instituto
Balseiro (1995-agosto de 2001). Título: Modelización de la dinámica
espacio-temporal del laser con realimentación óptica. Calificación:
Sobresaliente. (A. A. Duarte acepto una beca de la Fundación Fullbright para
continuar estudios en Cornell University).
- -
- Supervisor de Martín Zimmermann, Investigador Asistente, CONICET.
- -
- Director de tesis de doctorado de Federico Castez. Título: Dinámica de
interfaces en problemas de interés en nanociencia
( Becario del proyecto FONCYT 6-5030, becario CONICET),
(Feb. 2001 - Diciembre 2005). Universidad Nacional de La Plata. (Castez
continuó su carrera con una beca postdoctoral del CONICET).
- -
- Director PostDoctorado de Marcelo Javier Otero (Doctor en Química.
Octubre 2003-Septiembre 2005). Becario de CONICET.
- -
- Director de Marcelo Javier Otero, Investigador Asistente, CONICET,
Octubre 2005 -2010.
- -
- Director de beca (Agencia) de Daniel Dos Santos, biólogo (Junio de
2005-Enero de 2006): Regresó a su provincia por razones personales.
- -
- Director de beca de postdoctorado (ANPCyT) de María Laura Fernández
(Lic. en biología, Dra. en bioquímica), desde Junio de 2006 a Agosto 2007.
Ingresó al CONICET.
- -
- Director de Paula Bergero, becaria postdoctoral CONICET. Mayo 2008s -
Diciembre 2010. Ingresó al CONICET.
- -
- Director de la tesis de doctorado de Victoria Romeo Aznar, becaria de
CONICET, 1ero de abril de 2010 al 31 marzo de 2015. Tesis: Biología teórica,
modelo y experimentos aplicados al entendimiento de la dinámica del mosquito
Aedes aegypti. Co-directora: Dra. Sylvia Fischer. Continuó con una beca
postdoctoreal del CONICET.
- H. G. Solari, M. A. Natiello and G. B. Mindlin.
Nonlinear Dynamics.
A two way trip from physics to math.
Institute of Physics Publishing (IOP), Bristol (England, 1996),
388 páginas. ISBN 0 7503 0379 4 and 0 7503 0380 8, catálogo QC20.7.N6S65
- M.A. Natiello and H, G. Solari. The User's Approach to Topological
Methods in
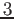 -D Dynamical Systems. World Publisher, Singapore, 2007.
ISBN-13 978 981 270 380 4
-D Dynamical Systems. World Publisher, Singapore, 2007.
ISBN-13 978 981 270 380 4
- Hernán G. Solari and Mario A. Natiello. Lasers. Fitzroy
Dearborn Encyclopedia of Nonlinear Science, Alwyn Scott Editor, New York and
London: Routledge, 2004. ISBN 1 57958 385 7
- Mario A. Natiello and Hernán G. Solari. Winding numbers. Fitzroy Dearborn Encyclopedia of Nonlinear Science, Alwyn Scott Editor, New
York and London: Routledge, 2004. ISBN 1 57958 385 7
- Mario Natiello and Hernán Solari. A Braided View of a Knotty Story.
Topology and Dynamics of Chaos: In Celebration of Robert Gilmore's 70th
birthday (World Scientific Series on Nonlinear Science, Series a). C. Letellier and R Gilmore (Editores). ISBN: 978-981-4434-85-0 (2013)
- Hernán G Solari. Robet Gilmore, a Portrait.
Topology and Dynamics of Chaos: In Celebration of Robert Gilmore's 70th
birthday (World Scientific Series on Nonlinear Science, Series a). C. Letellier and R. Gilmore (Editores) ISBN: 978-981-4434-85-0 (2013)
- Licenciatura. Fluctuaciones de presión en resalto
hidráulico libre y forzado. FCEN-UBA, 1978.
- Doctorado. Dinámica variacional en el problema de
muchos cuerpos: el tratamiento de las simetrías. FCEN -
UBA, 1984.
- E. S. Hernández and H. G. Solari. Irreversible
Dynamics of Quasispin systems. Physical Review C 25,
2087 (1982).
- H. G. Solari and E. S. Hernández. Quasispin dynamics
beyond the Bloch sphere: Exact versus Time-dependent Hartree-
Fock evolution. Physical Review C 26, 2310, (1982).
- E. S. Hernández and H. G. Solari. Kinetic parameters
in the nuclear Fermi gas model at finite temperature. Nuclear
Physics A 397, 115 (1983).
- H. G. Solari and E. S. Hernández. Symmetry conserving
variational dynamics: Application to quasispin systems.
Physical Review C 28, 2472 (1983).
- H. G. Solari and E. S. Hernández. Study of symmetry
breaking in the TDHF calculations. Z. Physik A 321, 155
(1985).
- H. G. Solari and E. S. Hernández. On the possibility
of dynamical symmetry restoration in the Gaussian overlap
hypothetis. Physical Review C 32, 462 (1985).
- H. G. Solari. Glauber's coherent states and the
semiclassical propagator. J. Mathematical Physics 27,
1351 (1986).
- D. Jezek, E. S. Hernández and H. G. Solari. Geometry
and time scales of selfconsistent orbits in a modified SU(2)
model. Physical Review C 34, 462 (1986).
- H. G. Solari. Semiclassical treatment of spin systems by
means of coherent states. J. Mathematical Physics 28,
1097 (1987).
- H. G. Solari, R. Gilmore and M. Vallieres. U(12)
Systematic in nuclei. Physical Review C 35, 320 (1987).
- H. G. Solari, E. Eschenazi, R. Gilmore and J. Tredicce.
Influence of coexisting attractors on the dynamics of a laser
system. Optics Communications 64, 49 (1987).
- H. G. Solari and R. Gilmore. Relative rotation rates for
driven dynamical systems. Physical Review A 37,
3096-3109 (1988).
- H. G. Solari and R. Gilmore. The organization of
periodic orbits in the Duffing oscillator. Physical Review
A 38, 1566 (1988).
- E. Eschenazi, H. G. Solari and R. Gilmore. Global
organization of basins of attraction in a driven dynamical
system. Physical Review A 39, 2609 (1989).
- H. G. Solari and R. Gilmore. Reduction of the Maxwell-
Bloch equation to a standard form. Optics Communications 71, 85 (1989).
- H. G. Solari and R. Gilmore. Dynamics in the transverse
section of a
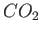 laser. Journal of the Optical Society of
America B7, 828 (1990).
laser. Journal of the Optical Society of
America B7, 828 (1990).
- N. B. Tufilaro, H. G. Solari, G. B. Mindlin and R.
Gilmore. Relative Rotation Rates: Fingerprints for strange
attractors. Physical Review A 41, 5717 (1990).
- Classification of strange attractors by integers. G. B.
Mindlin, X.-J. Hou, H. G. Solari, R. Gilmore and N. B.
Tufilaro. Physical Review Letters 64, 2350 (1990).
- Symmetry breaking in a laser: the experimental side. C.
Green, G. B. Mindlin, E. J. D'Angelo, H. G. Solari and J. R.
Tredicce. Phys. Rev. Lett. 65, 3124 (1990).
- Am eficient algorithm for fast O(N*ln(N)) box counting.
X-J. Hou, R. Gilmore, G. B. Mindlin and H. G. Solari. Physics
Letters A 151, 43 (1990).
- G. B. Mindlin, H. G. Solari, M. A. Natiello, R. Gilmore
and X-J. Hou. Topological analysis of chaotic time series data
from the Belousov-Zhabotinskii reaction. Journal of Nonlinear
Science 1 147 (1991).
- Structure of chaos in the laser with saturable absorber.
F. Papoff, A. Fioretti, E. Arimondo, G. B. Mindlin, H. G.
Solari and R. Gilmore. Phys. Rev. Letters 68, 1128 (1992).
- R. Gilmore, H. G. Solari and S. K. Kim. Algebraic Description of
the Quantum Defect. Foundations of Physics, 23, 873 (1993).
- B. G. Mindlin, R. López Ruiz, Hernán G. Solari and R. Gilmore.
Horseshoe Implications. Phys. Rev. E48, 4297 (1993).
- P. T. Boyd, B. G. Mindlin, R. Gilmore and H. G. Solari.
Topological Analysis of Chaotic Orbits: Hyperion.
Astrophysical Journal 431, 425 (1994).
- Remarks on braids and periodic orbits. M. A. Natiello
and H. G. Solari. Jour. of Knot Theory and its Ramifications 3,
511-529 (1994).
- Laser with injected signal: the perturbation of an
invariant circle. H. G. Solari and G. L. Oppo. Optics Communications 111,
173-190 (1994).
- G. B. Mindlin and H. G. Solari. Topologically Inequivalent Embeddings,
Phys. Rev. E52, 1497 (1995)
- H. G. Solari, M. A. Natiello and M. Vázquez.
Braids on the Poincaré section: A laser example. Phys. Rev. E. 54,
3185 (1996).
- Tori and Klein bottles in four dimensional chaotic flows.
B. G. Mindlin and H. G. Solari. Physica D 102, 177 (1997).
- H. G. Solari and B. G. Mindlin.
Quasicrystals and strong interactions between square modes.
Phys. Rev. E 56, 1853 (1997).
- M. Zimmermann, M. A. Natiello and H. G. Solari.
Sil'nikov-Saddle-node interaction near a codimension 2
bifurcation: Laser with injected signal. Physica D 109 (1997) 293-314.
- A. Duarte and H. G. Solari. Modelling the spatio-temporal
dynamics of semiconductor lasers. Optics Comm. 144, 99-108 (1997).
- A. Duarte and H. G. Solari. The metamorphosis of the monochromatic
spectrum in a double-cavity laser as a function of the feedback rate. Phys.
Rev. A 58 614-619 (1998).
- A. A. Duarte and H. G. Solari. Stability properties of the monochromatic
spectrum in a double-cavity laser. Phys. Rev. A60, 2403-2412 (1999).
- J. P. Aparicio and H. G. Solari. Sustained oscillations in stochastic
systems. Mathematical Biosciences 169, 15-25 (2001).
- J. P. Aparicio and H. G. Solari. Population dynamics: a Poissonian
approximation and its relation to the Langevin method. Phys. Rev.
Lett. 86, 4183-4186 (2001).
- Alejandro A. Duarte and Hernán G. Solari. The Slowly Varying
Envelop Approximation in the Laser with Optical Feedback.
Phys. Rev. A 64 33803, (2001).
- M. G. Zimmermann, M. A. Natiello and H. G. Solari. Global
bifurcations in a Laser with injected signal: beyond Adler's
approximation, Chaos 11, 500-513 (2001).
- Pablo F. J. de Leon, Ezequiel V. Albano, R. C. Salvarezza, and H. G.
Solari. Interface dynamics for copper electrodeposition: The role of organic
additives in the growth mode. Physical Review E 66, 042601 (2002).
- H. G. Solari y M. A. Natiello. Stochastic population dynamics:
the Poisson approximation. Physical Review E 67 031918 (2003).
- Marcos F. Castez, Bárbara Blum, Roberto C. Salvarezza and
Hernán G. Solari. Dynamics of solid growth under gravitational field:
Influence of the formation of a diffusive layer. Physical Review E 67,
061605 (2003).
- J. P. Aparicio, Hernán G Solari and Never Bonino. Competition and
coexistence in host-parasite systems: the myxomatosis case. Population Ecology,
46, 71 - 85, (2004).
- Marcos F. Castez, Roberto C. Salvarezza Hernán G. Solari. Probing
Universality classes in Solid-on-Solid deposition. Phys. Rev. E 70 011606 (2004).
- H. G. Solari y M. A. Natiello. Minimal Periodic Orbit Structure of
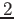 -Dimensional Homeomorphisms. Journal of Nonlinear Science, 15(3),
183-222, 2005.
-Dimensional Homeomorphisms. Journal of Nonlinear Science, 15(3),
183-222, 2005.
- Marcos F. Castez, Mariano H. Fonticelli, Omar Azzaroni, Luis Vázquez,
Roberto C. Salvarezza y Hernán G. Solari. Pattern preserving deposition:
experimental results and modeling. Applied Physics Letters, 87, 123104,
2005.
- J. P. Aparicio, H. G. Solari y N. A. Bonino. Perspectivas Teóricas Sobre
la Dinámica de la Mixomatosis con Aplicaciones en Control Biológico. Ecología
Austral 16, 15-28 (2006).
- M Otero, H. G. Solari and N. Schweigmann. A stochastic population
dynamics model for Aedes aegypti: formulation and application to a city
with temperate climate. Bulletin of Mathematical Biology, 68,
1945-1974 (2006).
- Marcos F. Castez, Roberto C. Salvarezza and Hernán G. Solari.
Modeling growth from the vapor and thermal annealing on micro/nano
patterned substrates. Physical Review E 73, 011607, 2006.
- M. A. Natiello and H. G. Solari. Blowing-up of deterministic fixed
points in stochastic population dynamics. Mathematical biosciences 209,
319-335, 2007. (http://dx.doi.org/10.1016/j.mbs.2007.02.002)
- M. Otero, H.G. Solari and N Schweigmann. A stochastic spatial
dynamical model for Aedes aegypti. Bulletin of Mathematical Biology
70, 1297-1325 (2008).
- M. A. Natiello and H. G. Solari. The topological reconstruction of forced
oscillators. Chaos, solitons and fractals 42, 2023-2034 (2009).
- M. J. Otero and H. G. Solari. Stochastic eco-epidemiological model of
dengue disease transmission by Aedes aegypti mosquito. Mathematical
Biosciences, 223, 32-46 (2010).
- Marcelo J Otero, Daniel Barmak, Claudio O Dorso, Hernán G Solar y Mario A
Natiello. Modeling Dengue Outbreaks. Mathematical Biosciences, 232, 87-95 (2011).
- D.H. Barmak, C.O. Dorso, M. Otero y H.G. Solari. Dengue epidemics
and human mobility. Physical Review E 84, 011901 (2011)
- Juan P. Aparicio, Mario A. Natiello y Hernán G Solari. The
quasi-deterministic limit of population dynamics. Int. J. Appl. Math. and
Statistics. 26(2), 30-45, 2012.
- V Romeo Aznar, Marcelo Otero, Maria Sol de Majo, Sylvia Fischer y Hernán
G Solari. Modeling the complex hatching and development of Aedes aegypti
in temperate climates. Ecological Modelling 253, 44-55 (2013).
- M L Fernández, M Otero, N Schweigmann y H G Solari. A mathematically
assisted reconstruction of the initial focus of the yellow fever outbreak in
Buenos Aires (1871). Papers in Physics, 2013 DOI: http://dx.doi.org/10.4279/pip.050002.
- Paula Bergero, Carlos A. Ruggerio, Ruben Lombardo, Nicolás Schweigmann,
Hernán Solari. Dispersal of Aedes aegypti: field study in temperate
areas and statistical approach. Journal of Vector Borne Diseases, September
(2013).
- D. Barmak, C. Dorso, M. Otero y H. G. Solari. Modelling interventions
during a dengue outbreak. Epidemiology and infection, 142, 545–561 (2014) doi:10.1017/S0950268813001301
- H. G. Solari and M. A. Natiello. Linear Processes in Stochastic
Population Dynamics. The Scientific World Journal - Journal of Probability and
Statistics, 2014, Article ID 873624, 15 pages. doi:10.1155/2014/873624.
- V Romeo Aznar, M S de Majo, S Fischer, D Francisco, MA Natiello and HG
Solari. A model for the development of Aedes (Stegomyia) aegypti as a
function of the available food. Journal of Theoretical Biology, aceptado,
Octubre 2014.
- H. G. Solari. Los límites de lo predecible (o el anagrama de Newton).
Ciencia Hoy, Vol. 6 (31), pag. 18 (1995).
- H.G. Solari. Una reconstrucción matematicamente asistida del foco inicial
de la epidemia de fiebre amarilla en Buenos Aires (1871). Ciencianet, enero de
2014. http://ciencianet.com.ar
- R. A. Lopardo y H. G. Solari. Fluctuaciones de presión
en la base de resalto libre. Anales del IX Congreso
Latinoamericano de Hidráulica, Mérida, Venezuela, June
1980.
- Winding numbers and collisions between attractors in a
laser system.
J. Tredicce, R. Gilmore, H. G. Solari
and E. Eschenazi. In Lecture Notes in Physics 282 ,273
(1987). F. Ehlotzky (Ed.).
- Lasers as a test bench for theories of non-equilibrium
structures. J. R. Tredicce, E. J. D'Angelo, C. Green, G. B.
Mindlin, L. M. Narducci, G. L. Oppo and H. G. Solari.
Proceedings of the workshop on Instabilities and
nonequilibrium structures, Valparaiso, Chile (1989). E.
Tirapegui and W. Zeller eds. Kluner Academic Publishers.
- Topological description of dynamical systems. R.
Gilmore, G. B. Mindlin and H. G. Solari. In Proceedings of
the International Workshop on Quantitative Measures of
Dynamical Complexity in Nonlinear Systems. N. B. Abraham, A.
M. Albano, A. Passamente and P. E. Rapp Eds. (Plenum, N.Y.
1990).
- Symmetry Breaking and Defect Mediated Turbulence in
Lasers. J. R. Tredicce, E. J. D'Angelo, C. Green, G. B.
Mindlin, L. N. Narducci, H. G. Solari, G. L. Oppo and L. Gil.
OSA Proceeding on Nonlinear Dynamics in Optical Systems, V7.
Ed. N. B. Abraham, E. M. Garmire and P. Mandel.
- Relative Rotation Rates for Driven Dynamical Systems. H.
G. Solari and R. Gilmore. In Proceedings of the International
Workshop on Quantitative Measures of Dynamical Complexity in
Nonlinear Systems. N. B. Abraham, A. M. Albano, A. Passamente
and P. E. Rapp Eds. (Plenum, N.Y. 1990).
- Comments on the topological organization of periodic
orbits. H. G. Solari, M. A. Natiello, G. B. Mindlin and R.
Gilmore. Proceedings of the workshop on Instabilities and
nonequilibrium structures, Valparaiso, Chile (1991). E.
Tirapegui and W. Zeller eds., Kluner Academic Publishers.
- H. G. Solari and M. A. Natiello.
Poisson approximation to density dependent stochastic processes.
A numerical implementation and test. Dynamical Systems from Number
Theory to Probability, Vaxjo Univ. Press. Ser. Math. Modelling,
7, 2003.
- R. Fernández, H. G. Solari y C. Faerman. Criterios
finales para el cálculo de protección radioquímica
del proyecto LPR. Reporte Interno CNEA PQ/IPQ 157 (1980).
- J. F. Heagy, G. B. Mindlin, H. G. Solari and R. Gilmore.
Integrability in Hilbert space: Classical and Quantum
Mechanics. Reporte interno, Drexel University, abril de 1989.
- H.G. Solari and F. Castez. On Langevin equations for fluctuating
surfaces, septiembre de 2006.
- V. Romeo Aznar, M. S. de Majo, S. Fischer, D Francisco, M.A. Natiello y
H. G. Solari. A model for the development of Aedes (Stegomyia) aegypti
as a function of the available food. 2014
- M.A. Natiello y H.G. Solari. Attempting to remove infinites from
divergent series: when Hardy will hardly help. 2014.
- M.A. Natiello y H.G. Solari. Average time in developmental sequences.
2014.
- *
- Reunión Nacional de Física (San Carlos de
Bariloche, diciembre de 1980).
- -
- Subdinámica de sistemas de cuasispin. E. S.
Hernández, H. G. Solari.
- *
- Reunión Nacional de Física (San Luis, noviembre
de 1981).
- -
- Teoría cinética de competencia de grados de
libertad nucleares. C. O. Dorso, E. S.
Hernández, H. G. Solari.
- -
- Validez de la representación de estados coherentes en
el modelo de Lipkin. E. S. Hernández, H. G.
Solari.
- -
- Cálculos macroscópicos del tiempo de relajación
del gas nucleónico. E. S. Hernández, H. G.
Solari.
- *
- V Reunión de trabajo de Física nuclear - CNEA.
(Chapadmalal, abril de 1982).
- -
- Aspectos conflictivos de la dinámica nuclear
colisional. C. O. Dorso, E. S. Hernández, H.
G. Solari.
- *
- Reunión Nacional de Física. (La Plata, diciembre
de 1982).
- -
- Aproximación semiclásica al estudio de la dinámica
nuclear: espacio de fases de estados coherentes.
H. G. Solari, E. S. Hernández.
- *
- Reunión Nacional de Física. (Tucumán, noviembre
de 1983).
- -
- Dinámica sobre variedades I. Restitución de las
simetrías en modelos de cuasispin. H. G.
Solari, E. S. Hernández.
- -
- Dinámica sobre variedades II. Evolución en ausencia
de simetrías. D. Jezek, E. S. Hernández,
H. G. Solari.
- *
- VIII Reunión de trabajo en física nuclear CNEA.
(junio de 1984).
- -
- Rupturas de simetrías en dinámica nuclear de
campo medio. H. G. Solari, E. S. Hernández.
- *
- 69 Reunión de la Asociacion de Física Argentina
(Buenos Aires, 1984).
- -
- Perturbaciones sobre trayectorias de Hartree-Fock en
ausencia de simetrías dinámicas. D. Jezek,
H. G. Solari, E. S. Hernández.
- *
- American Physical Society (Washington, D. C. April-May
1986).
- -
- F-spin systematics in nuclei. H. G. Solari,
M. Vallieres and R. Gilmore.
- *
- International Conference on Nuclear Structure,
Reactions and Symmetries. (Dubrovnik, Yugoslavia, June
1986).
- -
- U(12) Multiplets. H. G. Solari, R. Gilmore
and M. Vallieres.
- *
- Dynamics days. (La Jolla, California, enero 1987).
- -
- Influence of coexisting attractors on the dynamics of
lasers. H. G. Solari, E. Eschenazi, R. Gilmore
and J. Tredicce.
- *
- Dynamics Days. (Houston, Texas, 5-8 enero de 1988).
- -
- Relative rotation rates, symmetry and bifurcation
diagram in the Duffing oscillator. H. G. Solari
and R. Gilmore.
- -
- Nonlinear dynamics of a
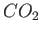 laser. H. G. Solari,
E. Eschenazi, J. R. Tredicce and R. Gilmore.
laser. H. G. Solari,
E. Eschenazi, J. R. Tredicce and R. Gilmore.
- -
- Basins of attraction: organization from birth to death.
E. Eschenazi, H. G. Solari and R. Gilmore.
- *
- Dynamics Days. (Houston, Texas, 4-7 enero de 1989).
- -
- Dynamics in the transverse section of a laser beam.
H. G. Solari and R. Gilmore.
- -
- Streching, Folding and Twisting in the Driven Duffing
Oscillator. R. Gilmore and H. G. Solari
- *
- International Workshop on Quantitative Meassures of
Dynamical Complexity in Nonlinear Systems. Bryn Mawr,
1990.
- -
- Topological description of dynamical systems.
R. Gilmore, G. B. Mindlin and H. G. Solari.
- -
- Relative Rotation Rates for Driven Dynamical Systems. H.
G. Solari and R. Gilmore.
- *
- SIAM congress on Dynamical Systems. Orlando, mayo de
1990.
- -
- Laser with inject signal: perturbation of an invariant
circle. H. G. Solari and Gian-Luca Oppo.
- -
- Classification of strange attractors by integers.
G. B. Mindlin, X-J. Hou, H. G. Solari, R. Gilmore
and N. B. Tufilaro.
- -
- Fingerprints for strange sets. N. B.
Tufilaro, H. G. Solari andR. Gilmore.
- *
- Nonlinear Dynamics in Optical Systems. Optical Society
of America Topic Meeting. Tulsa, Oklahoma, Jun 4-8 1990.
- -
- Codimension two bifurcation in a laser with injected
signal. G-L. Oppo and H. G. Solari.
- -
- Experimental studies of the evolution of laser intensity
profiles from Gaussian to turbulent. C. Green, E. J.
D'Angelo, G. B. Mindlin, L. M. Narducci, G. L. Oppo,
H. G. Solari and J. R. Tredicce.
- *
- Topological characterization of 3-dimensional
attractors. Jornadas MEDYFINOL, Mar del Plata, Argentina,
Junio de 1991.
- *
- VI Latin American Workshop on Nonlinear Phenomena,
Alta Gracia, Córdoba, Octubre de 1998.
- *
- Reunión Nacional de Física, Buenos Aires 2000.
- -
- Un modelo para el laser con reinyección óptica: lo
importante y lo accesorio. A. A. Duarte y H. G. Solari
- -
- Cocirculación de cepas virales de mixomatosis infectando
al conejo europeo. J. P. Aparicio y H. G. Solari.
- *
- Medyfinol: The importance of being discrete: Poisson
approximation to population dynamics. Colonia, Diciembre de 2002.
- *
- DIMACS: Workshop on the analogies between human and computer virus
(invitation only workshop). Rutgers University, July 10-14, 2002.
"The time evolution of small populations".
- *
- IX Latin American Workshop on Nonlinear Phenomena. San Carlos de
Bariloche, Argentina, 2005. Stochastic and deterministic population dynamics,
exploring their relation.
- *
- Reunión Nacional de Física (Merlo, spetiembre de 2006). Charla de la
división de Mecánica Estadística, Física no lineal y sistemas complejos.
Ecuaciones de Langevin en dinámica poblacional: ¿una ilusión universal?
- *
- Medyfinol: Modelling Aedes aegypti, the dengue and yellow
fever mosquito. Mar del Plata, 4-8 de Diciembre de 2006.
- *
- SIAM Conference on Applications of Dynamical Systems (DS07), May 28-June
1, 2007, Snowbird, Utah. H.G. Solari and M.A. Natiello. From
Time-series to Knots and Braids: the Programme in the Physical Sciences.
- *
- LERU workshop. Mario A Natiello and Hernán G Solari. When
science/teaching relations go wrong: The Hidden Curriculum. Febrero de 2008.
- *
- Reunión Nacional de Física: Lecciones de la historia a partir de
un modelo bio- matemático: la epidemia de fiebre amarilla, Buenos Aires 1871.
Agosto 2008.
- *
- Medyfinol: Lessons from a mathematical model for the big Yellow Fever
epidemic (Buenos Aires, 1871. 1-5 de Diciembre de 2008. Punta del Este,
Uruguay.
- *
- EARLI Mario A Natiello and Hernán G Solari. Changes
in the meaning of mathematical correctness during the enculturation of
graduate students in physics: conflicts and tensions. Agosto de 2007.
http://www.earli.org/resources/Abstracts%20Budapest%202007.pdf
- *
- Dynamics in systems biology H G Solari, M. Otero and M.L
Fernández. An Eco-Epidemiological Model for Dengue an Yellow Fever.
Applications to temperate regions. Aberdeen (Scotland), September 2009.
- *
- VI Jornadas de Mosquitos, Posadas, Septiembre de 2010
- Fernández M. Laura; Otero Marcelo; Schweigmann Nicolás; Solari Hernán G.
Modelo Matemático de Transmisión de fiebre amarilla incorporando la movilidad
humana. Simulación de la Epidemia Ocurrida en Buenos Aires en 1871.
- Bergero, Paula; Solari, Hernán; Schweigmann, Nicolás
Estudio de la Dispersión del Mosquito Aedes Aegypti hacia Ambientes Silvestres
- Ruggiero, Carlos: Beserra, Vanesa; Rodríguez, Patricia; DE Arcos Nieva,
María; Schweigmann; Nicolás; Solari, Hernán; Lombardo, Ruben.
Estudio de Dispersión de la Oviposición de Aedes aegypti en Ambiente Silvestre
Lindero a Área Urbana.
- Romeo Aznar, Victoria T., Solari, Hernán G.
El Efecto de la Lluvia sobre la Eclosión de Huevos de Aedes aegypti.
Estudio e Incorporación a un Modelo.
- *
- From laser dynamics to the topology pf chaos. Rouen, France, June 2011.
- H. G. Solari. The master’s use of the lapis philosophorum :
Turning ignorance into a great project (circa 1987).
- M. A. Natiello and H. G. Solari. A Braided View of a Knotty
Story
- *
- Comparison of two spatial models of Aedes aegypti population dynamics.
59th American Society of Tropical Medicine and Health Annual meeting,
Philadelphia, PA, USA. Legros M., Otero M., Solari H., Scott T.W.,
Gould F. and Lloyd A.L. (Diciembre 2011)
- *
- 5ta Escuela BIOMAT, La Falda, Córdoba, Agosto 2012. Lecciones aprendidas
en la construcción del modelo para Aedes aegypti Hernán G
Solari, Marcelo Otero, Sylvia Fischer, Nicolás Schweigmann, Victoria Romeo
Aznar y Mario Natiello.
- *
- 8vo Congreso Latinoamericano de Biomatemática, SOLABIMA 2013, Luján,
Argentina, 15 al 18 de octubre de 2013. Conferencia inaugural ``Reflexión: el
lugar de los modelos en la ciencia''.
- *
- 6ta Escuela BIOMAT, La Falda, Córdoba, Julio 2014. Curso de tres clases
Ense
Ánnnnnnnnanzas del modelo de Aedes aegypti y dengue (1. La filosofía detras
del modelo; 2. EL modelo; 3. Aprendiendo del fracaso)
Hernán G Solari, Nicolás Schweigmann, Sylvia Fischer, Marcelo
Otero, Paula Bergero, María Laura Fernández, Victoria Romeo Aznar, Mario
Natiello y Alejandro Romero.
- -
- IBM-2: SU(12)-based systematics. Department of Physics,
University of Pennsylvania, Enero de 1986.
- -
- Semiclassical approximation by means of coherent states.
Maryland University, Marzo de 1986.
- -
- Algebraic description of a CO2 laser. Department of
Chemistry, University of Pensylvania, Octubre de 1986.
- -
- Knots and links from experimental data. Bryn Mawr
College,
Septiembre de 1990.
- -
- Bifurcaciones, topología y dinámica no lineal.
Instituto de Astrofísica y Física del Espacio
(IAFE), Argentina, Octubre de 1990.
- -
- Sobre trenzas y nudos. Departamento de Física,
Universidad Nacional del Sur, Argentina, Marzo de 1991.
- -
- Study of singularities in a laser with injected
signal. Departamento de Química Cuántica,
Universidad de Uppsala, Suecia. Septiembre de 1991.
- -
- Patterns, dynamics, lasers and symmetries. Departamento
de Física, Universidad de Pisa, Italia. Septiembre de
1991.
- -
- Comments on the topological organization of periodic
orbits. H. G. Solari. Workshop on Instabilities and nonequilibrium
structures, Valparaiso, Chile (1991).
- -
- Dinámica en el laser con se
'Annnnnnnnnal inyectada.
Departamento de Física. Universidad de La República,
Montevideo, Uruguay, Agosto de 1992.
- -
- ... no se llevaron registros entre 1993 y 1995.
- -
- Bifurcaciones con simetrías. CNEA, septiembre de 1995.
- -
- Trenzas caóticas: obtención de la entropía topológica
a partir de datos experimentales. Encuentro Uruguayo de Sistemas
Dinámicos, Piriápolis, mayo de 1996.
- -
- Caos, crisis y otras metáforas no-lineales, Facultad de
Ciencias Económicas de la UBA, octubre de 1996.
- -
- Presente y futuro de la dinámica no-lineal. INIFTA, La Plata,
junio de 1998.
- -
- The metamorphosis of the monochromatic spectrum in a double-cavity laser.
IMEDEA, Palma de Mallorca, Espa
Ánnnnnnnnnna, May 1999.
- -
- The metamorphosis of the monochromatic spectrum in a laser with
optical feedback. Stockholm University, May 1999/
- -
- The time-evolution of small populations: stochastic dynamics
is not just determinism plus noise. Department of Mathematics, Lund
University, Sweden, May 2001.
- -
- The laser with optical feedback. Department of Mathematics,
Lund University, Sweden, May 2001.
- -
- The laser with optical feedback. Department of Mathematics, Lund
Univeristy, Sweden, May 2004.
- -
- Dinámica Poblacional. Departamenento de física, FCEN-UBA, 18 de marzo de
2004.
- -
- Aspectos sociales de la ciencia. Ciclo: Ciencia para quien,
FCEN-UBA, 2006. (Panel de tres expositores sobre evaluación en ciencia).
- -
- Grupo de física teórica, CNEA. Lecciones de la historia a partir de un
modelo bio- matemático: la epidemia de fiebre amarilla, Buenos Aires 1871.
Npoviembre de 2008.
- -
- An Eco-Epidemiological Model for Dengue and Yellow Fever:
Theoretical biology or applied mathematics?. Department of Mathematics, Lund
University, September 2009.
- -
- Mateadas científicas de la Universidad Nacional de General Sarmiento.
Cuestiones sociales en derredor de la fiebre amarilla y el dengue. Junio de
2012.
- -
- INTA Castelar (2012). Modelos Matemáticos en Epidemiología.
- -
- UNCP, Tandil (2014). La disputa por el conocimiento. Matemática pura vs
aplicada ¿Idealismo vs materialismo?
- -
- CNEA-Tandar (2014). El modelo de poblaciones de Aedes aegypti.
¿sirve para algo?
- An Experimental Approach to Nonlinear Dynamics and Chaos
by Nicholas B. Tufillaro, Tyler Abbot, Jeremiah Reilly.
- Chaos and Nonlinear Dynamics. Robert C. Hilborn, Oxford University
Press, New York. ISBN 0-19-508816-6
- Coping with chaos. E. Ott, T. Sawer and Y. York eds. John Wiley and
Sons. Reproduces Structure of chaos in the laser with saturable absorber.
F. Papoff, A. Fioretti, E. Arimondo, G. B. Mindlin, H. G. Solari and
R. Gilmore. Phys. Rev. Letters 68, 1128 (1992).
- H D I Abarbanel, R Brown, J J Sidorowich and L Sh Tsimring,
The Analysis of Observed Chaotic Data in Physical Systems,
Rev. Mod. Phys. 65, 1331, 1993.
- Analysis of observed Chaotic Data. Henry Abarbanel.
ISBN 0387983724.
- W. Ghrist , P.J. Holmes and M.C. Sullivan
Knots and Links in Three-Dimensional Flows, 1997. ISBN 3-540-62628-X
- R. Gilmore. Topological analysis of chaotic dynamical systems. Review
of Modern Physics 70, 1455-1530 (1998).
- M. Stone, Kee-Su Park and A. Garg. The semiclassical propagator for
spin coherent states. Journal of Mathematical Physics 41,
8025-8049 (2000).
Nota: la numeración de los trabajos se refiere a la lista de
trabajos publicados en revistas internacionales con proceso de
referato.
- Bernardo Gabriel Mindlin. El Dr. Mindlin fue dirigido por
Robert Gilmore (PhD) actuando yo como codirector como lo acreditan las
publicaciones en común de ese periodo [17-22, 24]. El Dr. Mindlin
ha tenido una brillante carrera como profesor primero en la
Universidad de Navarra (Espa
'Annnnnnnnnnna) y luego en la de Buenos Aires, se ha
hecho acreedor a varios premios y es sin duda uno de los mejores
investigadores del Departamento de Física de la FCEyN (UBA).
- Martín Zimmermann. El Dr. Zimmermann realizó su
trabajo de tesis de licenciatura bajo mi dirección. El trabajo
realizado se proyectó en su doctorado bajo la dirección del Dr.
Mario A. Natiello en la Universidad de Uppsala (ver [34]). El Dr.
Zimmermann realizó un postdoctorado en la Universidad de las Islas
Baleares para finalmente retornar al Departamento de Física de
la FCEyN (UBA) reincorporándose al grupo de trabajo. Sus intereses
actuales lo han llevado al estudio de problemas de
auto-organización en sistemas socio-económicos habiendo logrado
una buena repercusión con estos trabajos (ver Physical Review Focus
6, 28 (2000) [22 December 2000]. Stock Market: Follow the Leader, by
David Ehrenstein. http://focus.aps.org/v6/st28.html).
- Juan Pablo Aparicio. El Dr. Aparicio decidió reorientar
su carrera hacia temas de matemática aplicada a la biología al
realizar su doctorado. Finalizado el mismo tuvo la inusual
oportunidad de elegir entre varias ofertas de becas postdoctorales
optando por el Departamento de Bio-matemática de la Universidad de
Cornell, donde trabajó bajo la supervisión del Dr. Castillo
Chavez. Obtuvo las becas de postgrado nacional e internacional del
CONICET optando por regresar al país para trabajar junto al Dr.
Angel Capurro, decisión que se vió frustrada por el fallecimiento
del Dr. Capurro. Actualmente se interesa por temas de matemática
aplicada al estudio de problemas epidemiológicos, ecológicos y al
manejo de recursos naturales.
- Alejandro A. Duarte. El Licenciado Alejandro Duarte se
doctoró en el Instituo Balseiro en agosto de 2001. Sus intereses
personales lo han llevado a empe
Ánnnnnnnnnnnnar su voluntad en temas de
economía. En tal sentido renunció a su beca del CONICET
aprovechando una oportunidad de incorporarse al grupo de análisis
de riesgo y control del CITIBANK. Desde esa posición continuó y
completó su trabajo de tesis de doctorado. Finalmente obtuvo una
beca de la Fundación Fullbright para realizar un master en temas de
economía en la Universidad de Cornell (Agosto-2000). La meta
perseguida por el licenciado Duarte es lograr aplicar su formación
en el análisis de problemas dinámicos a temas de economía,
tanto en el ámbito académico como en el asesoramiento a empresas,
habiendo elegido sin duda un largo pero extremadamente serio camino
para el logro de sus objetivos.
The rise in popularity of dynamical systems theory, fueled largely by a
widespread interest in the phenomenon of chaos, has led to an increasing flood
of textbooks on the subject onto the market, and it would appear that any new
one would face stiff competition. However, the book under review occupies a
niche that is not well supplied; it is a graduate level book, aimed specifically
at physicists who want to apply die tools of nonlinear dynamics to their own
research problems. As such ¡t sets itself the ambitious targets of not only
describing nonlinear dynamics, but of presenting the main mathematical
techniques and of showing how these are applied in the investigation of
experimental and observational data. Since any one of these in itself could
(and currently does) form the subject matter of a book, ¡t is not to be expected
that the authors can provide a comprehensive and detailed coverage. What they
do provide is a stimulating and challenging book that conveys well the flavour
of nonlinear dynamics as an active area in physics, and that hopefully will
encourage physicists to acquire the ideas and apply them in a broad range of
contexts.
The style of the book is rather different to that of the more well established
books at this level, (notably J. Guckenheimer and P. Holmes's "Nonlinear
Oscillations, Dynamical Systems and Bifurcations of Vector Fields"): the
authors go to great lengths to set the theory in the context of physical
problems, describing how the problems engender and shape the theories and the
associated mathematics. This style of presentation leads them, for example,
to introduce homoclinic bifurcations in the context of numerical experiments
on the Lorenz system, to follow with a general discussion of global
bifurcations in which homoclinic tangles and horseshoes are introduced, and
then to give a more detailed discussion of horseshoes and their symbolic
dynamics. A more mathematically oriented presentation would probably have
taken these subjects in just the reverse order. Other manifestations of the
authors' theme of nonlinear dynamics as a tool for physicists are: the
inclusion of a chapter on numerical experiments, illustrating how such
simulations are an important source of information about models, prompting and
guiding the subsequent theoretical analysis; and the inclusion of a chapter on
how experimental data can be manipulated to investigate the dynamics of the
underlying system, using embedding techniques.
Most of the usual topics in nonlinear dynarnics get an airing: there is a
general introductory chapter describing flows, orbits, attractors, Poincaré
sections and so on, and there are chapters on stability, local bifurcations,
global bifurcations, maps of the interval, and averaging methods. Some less
common topics also make an appearance: there is a chapter on the role of
symmetry in bifurcations, and one on the topological properties of three
dimensional flows.
With this much ground to cover ¡t is inevitable that the authors spread
themselves rather thinly at times. The discussion of some of the mathematical
tools (such as local Poincaré maps, or Liapunov exponents)
is sketchy, and could leave the uninitiated reader unsure about how these
things are actually used. Since this book is aimed primarily at physicists
and other physical scientists there is very little in the way of formal proof;
the more intuitive arguments which are presented instead will appeal to many,
but may not be to everyone's taste, especially not those with a more
mathematical bent. Part of the answer to this lies in the remark in the
Preface that "this is a book to be read with paper and pencil at hand". This
is certainly true: the reader is often left to fill in the details for
him/herself, and will no doubt get the most out of the book by doing so. But
as well as paper and pencil, occasional reference to Guckenheimer and Holmes
might be useful to flesh out some of the arguments.
Apart from a willingness to put pencil to paper, the book requires a grounding
in elementary topology, (open and closed sets, and homeomorphisms are talked
about with little preamble). For some physics graduates this could be a
problem, but a standard ancillary analysis course, up to and including metric
spaces, would probably provide sufficient background. Some familiarity with
ordinary differential equations would be helpful, as would some knowledge of
linear systems.
Though ¡t makes fairly serious demands on the reader, the research physicist
who works through this book will gain rich rewards in a broad familiarity with
nonlinear dynamics and its applications. lt. might even cause them to look at
the phenomena they study in a new way.
Jerry Huke, Mathematics Department, University of Manchester Institute of
Science and Technology.
email: J. P. Huke @umist.ac.uk.
The authors of this graduate text promise to provide the reader with the
mathematical tools of nonlinear dynamics needed to tackle problems in all
areas of physics. Topies covered are: introductions to linear and nonlinear
dynamics and the elements of their description, elementary stability theory,
two- and three-dimensional-flow, local and global bifurcations, horseshoes,
and the extraction of qualitative dynamical behavior from recorded data.
The initial promise, however, is not kept: this is mainly a descriptive text
about nonlinear physics with some additional equations and graphs. In this
respect the book succeeds quite well: where other texts are often too brief
in their discussion of methods and results, it provides extensive discussion
of these topics, which makes it an ideal companion of the standard textbooks.
K. Brod (Wiesbaden).
Perhaps surprisingly, given its origins in celestial mechanics, modern
nonlinear dynamics has never made it into the core physics curriculum. As the
authors of Nonlinear Dynamics: a Two-Way Trip from Physics to Math, observe in
the Preface, quantum mechanics, which also has its origins around the turn of
the century, caught the attention of the physics community and quantum
mechanics deals with linear operators on linear (Hilbert) spaces after all.
In some of the more phenmenological areas of physics, however, nonlinear
dynamics has found fertil soil: fluid dynamics, plasma physics, mesoscopic
physics (quantum chaos), to name a few. The authors of the present book are
active in the field of laser dynamics. and it shows.
Reflecting the increasing interest in the application of dynamical systems to
virtually every field of researeh, recent years have seen a proliferation of
Books pitched at the advanced undergraduate/first-year graduate level. Books
presenting the key elements of theory are, for example, Rasband [1], Hale &
Koccak [2], Ott [3], Strogatz [4], Glendinning [5] and Verhulst [6]. Besides
these general texts there is a good helping of books aimed at specialised
audiences of a more pure (e.g., Palis & Takens [7]) or more applied (e.g.,
Moon [8], Schuster [9]) flavour. The book under review is directed to
begining graduate student and reaserchers in physics, mathematics and
engineering, but will mostly-appeal to physicists. It is meant to be a
comprehensive text. In 16 chapters the 350 pages or so cover a wide range of
topics. The somewhat enigmatic subtitle, as explained in the Preface, refers
to the hand-in-hand approach of mathematics and physics in the evolution of
problems and solutions (i.e., theories) in our sciencific nquires. The pairs
classical mechanics-calculus (Newton), quantum mechanics-Hilbert spaces (Von
Neumann) and nonlinear dynamics-topology (Poincaré) serve as examples.
The style of the book is informal and people should not be put off by the
message on the back cover that "The book presents rigorous results..." A fair
selection of key results is presented in the form of theorems but proofs are
omitted (or sketched, in rare cases). References to the literature are given
instead. The organisation of the material is well thought-out and each chapter
ends with a brief summary.
The story begins in Chapter 1 with a description of some experiments
illustrating that physical systems can show markedly different behaviour as
parameters (physical control variables) are varied. As examples we are offered
turbulent fluids, modulated lasers and symmetry-breaking plasmas. In the next
six chapters the elementary theory of dynamical systems is presented: linear
dynamics, limit sets, invariant manifolds, Poincaré sections, (structural,
Lyapunov) stability, two-dimensional flows and bifurcations. By then we have
also had a closer look at some mathematical models underlying the phenomena
reviewed in Chapter 1. The chapter on two-dimensional flows essentially deals
with the Poincaré-Bendixon theorem classifying the possible limit sets of
such systems. Some unnecessary confusion is caused by the fact that there are
two results presented under the name Poincaré-Bendixson Theorem, one a,
lemma to the other.
Chapter 7 on birfurcations first introduces centre manifold reduction and
normal forms and then gives a survey of the simple local codimension-one
bifurcations. All of this for maps as well as flows. Relatively match time is
spent, on discussing the delicated Hopf biftircation for maps (treatment of
the stringly resonant cases is deferred till after the introduction of
averaging in Chapter 14). This bnifurcation, which also goes under the name of
Naimar-Sacker bifurcation, is called a codimension-two bifurcation by the
authors, while only its codimension one cases are treated. Indeed,
codimension-two bifurcations receive hardly any attention at all in the book.
Chapter 8 presents results of numerical simulations of some low-dimensional
continuous and discrete systems focusing on period-doubling cascades,
mode-locking, the Lorenz attractor and crisis. Here we have our first
encounter with chaotic dynamics, loosely defined in the text as the aperiodic
behaviour observed in numerical experiments. Chaos is not popularised in the
book. Rather, the authors are interested in the intrincate structure of
perriodic orbits underlying complex behaviour and, in the following four
chapters, quickly move on to discussing homoclinic tangles, horseshoes,
one-dimensional maps, knots and braids. This part of the book is
topological/combinatorial in nature. The chapter on the application of the
techniques of knots and braids, the authors' own expertise, is one of the best
of the book. The subjet is still the domain of a rather specialised group of
researchers (many of them working in laser dynamics) and is not found in many
other books. The methods of knots and braids can be very powerful in
predicting the existence of certain periodic orbits, much like kneading theory
does in unimodal maps. Unfortunately, they are in large part restricted to
three-dimensional flows with globally defined Poincaré sections, which in
practise often means periodically perturbed planar systems.
The final four chapters cover such miscellaneous subjects as experimental time
series, Lyapunov exponents, dimensions and entropy, averaging (used to study
subharmonic resonance and the strongly resonat Hopf bifurcation). The last
chapter on global bifurcations takes up the line of the Chapters 9-12 and
treats horseshoe creation in systems with Silnikov-type bifurcations, both
with and without symmetry.
My main criticism is that, partly due to the wide spread of material, the
discussion tends to remain too superficial for a textbook. This is made worse
by the fact that the text contains an insufficient number of examples, which
otherwise could have given the book a more explicit character. For instance,
there are no examples illustrating the Poincaré-Bendixon and Hopf
bifurcation results (either for maps of flows). Instead, the pages are richly
sprinkled with exercises, to which parts of the main line of development are
relegated. The authors seem to find encouragment for this strategy in a quote
by Von Humboldt, but the mathematically inclined or the not so easily
convinced might be less quickly reassured. Those will benefit from reading one
or two other books simultaneously. On the other hand, the laser models thrpwn
in at several places provide useful non-standard illustrations of some
interesting dynamical phenomena (subharmonic resonance, Silnikov bifurcation).
Despite the book's wide scope, some areas of nonlinear dynamics, inevitably,
go uncovered. There is virtually nothing on conservative (Hamiltonian) systems
abd (multi)fractals (although Cantor sets are discussed). Nothing will be
found on numerical methods (apart from time series analysis), control of
chaos, PDEs or inifinite dimensional dynamical systems, pattern formation,
complexity or quantum chaos. Since dynamical systems theory is the geometrical
approach to differential equations (and iterated maps), figures can be
extremely helpful in coveying ideas. In this respect the book is sufficiently
illustrated. There is an adecuate list of references.
In conclusion, as someone versed in nonlinear dynamics (and with a background
in physics) I enjoyed reading the book, partly because an intuitive account
often goes down better than a detailed mathematical exposition. The student,
though, might quickly be seen grabbing at mathematically more explicit
accompanying material.
Das Buch richtet sich an Naturwissenschaftier und fortgeschrittene
Studenten nút eincm Hinte@nd in der Mathematik oder Physik. Der
Leser wird durch die Darstellung von Falibeispicien und eine gro8e
Zahl von Obungsaufgaben an die Fragestel]ungen der nichtlinearen
Dynamik herapgeführ, und mit wichtigen mathematischen Resultaten und
Methoden vertraut gemacht. Dabei ist der Text als Arbeitsbuch
gedacht, anhand dessen man sich das Wissen für eigene Forschung in
diesem erarbeiten soll.
Autoren entwickeln die Theorie dynanúscher ysteme induktiv anhand von
physikalischen men. Es werden ausschlieblich Beispiele t dircktem
physikalischen Bezug zur Illustrativon Sachverhalten herangezogen und
keine
Definitionen ohne eine direktc physikalische Motivation
gegeben. Ein grol3er Te¡] der Beispiele bezieht sich auf
unterschiedlich getriebene Lasersysteme. Sehr ausfúhrlich werden die
Stabilitát von L¿jsungen und Bifurkationen diskutiert, sowie die
topologische Klassifizíerung von niedrigdimensionalen Flüssen und
damit asnoziierter Abbildungen. Andererseits sind kiassische
Resultate, wie die Kaplan-Yorke-Forrnel für die fraktale Dimension
eines chaotischen Attraktors, nicht erwáhnt.
Für den erfahrenen Leser ergeben sich durch die an Anwendungen
orientarte Darstellung bisweilen interessante Einblicke in Probleme
und Einschránkungen be¡ der Anwendung rnathematischer Resultate auf
physikalische Probleme. Alierdings findet man nqr schwer Zugang zu
dem Buch. Die Darstellung der Theorie leidet, da die Begriffsbildung
der Autoren teilweise unklar ist. Einige zentrale Begriffe werden
nur indirckt durch den Kontext, in den¡ die Autoren sie verwenden,
oder durch Beispiele eingefiihrt.
Wegen dieser didaktischen Schwáchen und der in meinen Augen
eigenwilligen Auswahl der Themen würde ich das Buch als EinfiMng in
die nichtlineare Dynan-dk nur bedingt empfehlen. Leser rait
erheblicher Erfahrung in dem Gebiet finden jedoch in einigen der
weiterfúhrenden Kapite¡ interessante Anregungen.
J. Volimer, Essen
Another textbook on Nonlinear Dynamics? Some might feel that there are enough
already. This book does an excellent job, however, and merits a place alongside
the best of those aimed at physicists. Starting from motivating problems in
population dynamics, fluid mechanics, laser physics and plasma physics, the
authors develop the philosophy, tools and results of dynamical systems theory
in a clear and structured way. Unlike some of the purely mathematical texts
(e.g. Katok and Hasselblatt), this book gives full weight to the aspects that
have been found to be of use in scientific applications. These include centre
manifold reduction, bifurcation theory, averaging, Melnikov's method, effects
of symmetry and near-symmetry, knots and links in 3D systems, and time series
analysis.
On the whole-the book is accurate, but there are a few points where ¡t is
weak. The "open problem" on p.65 about existence of a global Poincaré section
was given an answer by Fried in Topology 21 (1982). There are obstructions to
smooth linearization not only for saddles (p.77), but also for sinks and
sources (see examples in books by Arrowsmith and Place, Wiggins, Glendinning and
others). The torsion recursion relationship on p. 142 can be derived from the
R* operator of kneading theory. Appeal to the Hartmann-Grobman theorem on p.313
is insufficient for analysis of homoclinic bifurcations: a smooth linearization
theorem or at least a smooth normal fórm is required. Nonetheless, I would
recommend the book to any physicist (or scientist) who wishes to obtain a
grounding in the theory and practice of nonlinear dynamics. It would also make
an excellent text for an advanced undergraduate or postgraduate course.
R. S. MACKAY (University of Cambridge)


- *
- Lenguajes de programación BASIC, ALGOL, FORTRAN,
PASCAL y C. Programación para X-Windows.
- *
- Experiencia como System Manager en networks de Workstations Unix.
- *
- Experiencia en la utilización de equipos de
computación en cálculos científicos y técnicos.
(Equipos digital PDP-11/45, Hewlett Packard 9831 A, Nova Data,
IBM 370, VAX 780, IBM 3090, CRAY XMP, SUN-4 y Personal
Computers).
- *
- Dominio del idioma inglés y lectura en francés.
- Cinturón negro de yudo. Campeón argentino en
una oportunidad, subcampeón en dos oportunidades.
- Profesor superior de Guitarra, conservatorio Santa Cecilia.
- Estudioso del comportamiento animal, entrena sus perros de trineo
(Malamutes de Alaska).
- Practica equitación en forma recreativa (adiestramiento y salto).
CV
This document was generated using the
LaTeX2HTML translator Version 2008 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -unsegment -split 0 -iso_language ES.AR CV.tex
The translation was initiated by Hernán Gustavo Solari on 2015-04-04
Hernán Gustavo Solari
2015-04-04

