Problema 7: Defectos de Frenkel¶
Una red cristalina perfecta está formada por 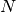 átomos de la
misma especie. Si se extraen
átomos de la
misma especie. Si se extraen 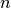 átomos de sus lugares en la
red (con
átomos de sus lugares en la
red (con 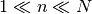 ) y se los coloca en posiciones
intersticiales, se obtienen
) y se los coloca en posiciones
intersticiales, se obtienen 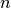 defectos de tipo Frenkel. El
número
defectos de tipo Frenkel. El
número 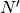 0 de posiciones intersticiales en la red es del
orden de magnitud de
0 de posiciones intersticiales en la red es del
orden de magnitud de 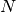 . Sea
. Sea 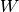 la energía necesaria
para producir un defecto. Halle el valor de
la energía necesaria
para producir un defecto. Halle el valor de 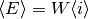 y de allí muestre que
y de allí muestre que
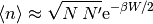
Grafique cualitativamente 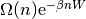 en
función de
en
función de 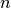 . Resuelva este problema tanto en el ensamble
microcanónico como en el canónico.
. Resuelva este problema tanto en el ensamble
microcanónico como en el canónico.
Ensamble microcanónico¶
En el ensamble microcanónico tenemos que calcular 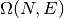 , y a partir de esta superficie obtenemos la entropía:
, y a partir de esta superficie obtenemos la entropía:
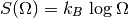
Queremos hallar los estados compatibles con una energía 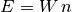 . Si quitamos
. Si quitamos 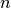 átomos de sus posiciones de la red,
tenemos
átomos de sus posiciones de la red,
tenemos 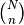 formas de quitar los átomos y
formas de quitar los átomos y 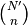 formas de escoger qué posiciones intersticiales
ocupamos. Así, la superficie es:
formas de escoger qué posiciones intersticiales
ocupamos. Así, la superficie es:
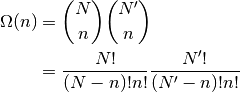
y calculamos la entropía:
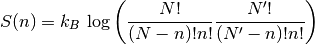
Con la aproximación en la que 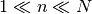 , todos los términos
son muy grandes, y podemos aplicar la aproximación de Stirling.
, todos los términos
son muy grandes, y podemos aplicar la aproximación de Stirling.
![S(n) \approx S_S(n) = k_B\,[&N \log N - N - n \log n + n - (N - n)
\log (N - n) + (N - n) + \\
+&N' \log N' - N' - n \log n + n - (N' - n)
\log (N' - n) + (N' - n)]](../../_images/math/44959ea6aa9aa95be7d3a6665f700d041036fe50.png)
con las simplificaciones típicas de números combinatorios (ver
Apéndice), definiendo 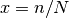 ,
, 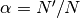 , resulta
, resulta
(1)![S_S(x) = - k_B[&N(x \log{x} + (1 - x) \log{(1-x)}) \\
+&N'\left(\frac{x}{\alpha} \log{\frac{x}{\alpha}} + \left(1 -
\frac{x}{\alpha}\right) \log\left(1-\frac{x}{\alpha}\right)\right)]](../../_images/math/4f2848f4080f433b4dcf59a8d496fac139dc6327.png)
Si queremos encontrar la temperatura, tenemos que calcular la derivada de la entropía respecto de la energía. Como hicimos en Problema 4: Dos niveles,
(2)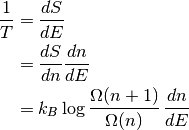
En nuestro caso, 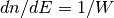 y
y
(3)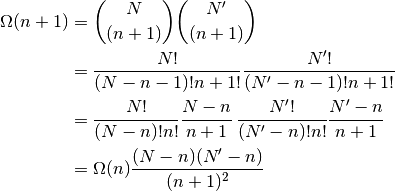
Queda la temperatura, entonces
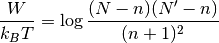
De aquí despejamos 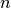 , definiendo
, definiendo 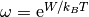 .
.
(4)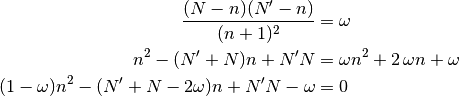
Y obtenemos
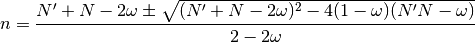
En el límite termodinámico, 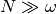 , y la expresión para
, y la expresión para
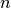 queda
queda
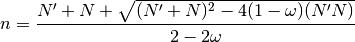
Finalmente, veamos cómo se comporta 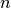 el régimen que nos piden
en el enunciado,
el régimen que nos piden
en el enunciado, 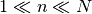 . Parece intuitivo notar que esta
aproximación es para temperaturas bajas. En este caso, podemos hacer
la aproximación en (4)
. Parece intuitivo notar que esta
aproximación es para temperaturas bajas. En este caso, podemos hacer
la aproximación en (4)
(5)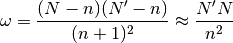
y despejando, llegamos al resultado
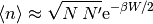
Podemos ver en qué régimen estas dos expresiones (4) y
(5) son parecidas, con 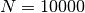 , y
, y
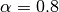 :
:
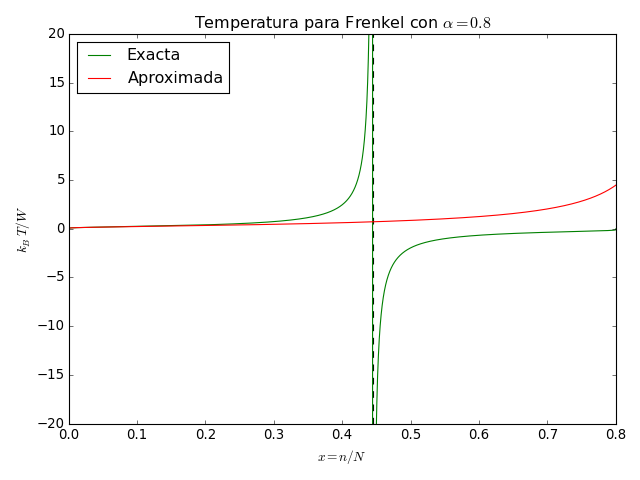
import numpy as np
import pylab as pl
N = 10000
alpha = 0.8
xc = alpha/(alpha + 1)
pmax = min(alpha, 1)
x = np.linspace(0, pmax, pmax * N)
Tex = -1/np.log((x+1/N)**2/((1-x)*(alpha-x)))
Tap = -1/np.log(x**2/alpha)
pl.figure()
pl.plot([xc, xc], [-20, 20], 'k--')
pl.plot(x, Tex, 'g-', label='Exacta')
pl.plot(x, Tap, 'r-', label='Aproximada')
pl.xlabel(r'$x = n/N$')
pl.ylabel(r'$k_BT/W$')
pl.ylim((-20, 20))
pl.xlim((0, pmax))
pl.title(r'Temperatura para Frenkel con $\alpha = {0}$'.format(alpha))
pl.tight_layout()
pl.legend(loc="upper left")
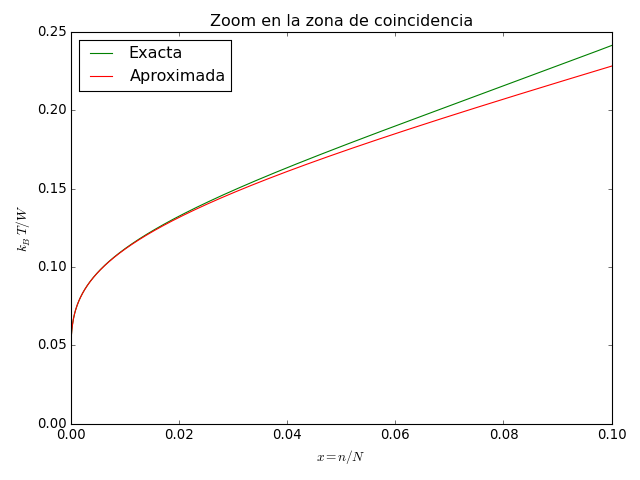
pl.figure()
pl.plot(x, Tex, 'g-', label='Exacta')
pl.plot(x, Tap, 'r-', label='Aproximada')
pl.xlabel(r'$x = n/N$')
pl.ylabel(r'$k_BT/W$')
pl.ylim((0, 0.25))
pl.xlim((0, 0.1))
pl.title(r'Zoom en la zona de coincidencia'.format(N))
pl.tight_layout()
pl.legend(loc='upper left')
Aparece nuevamente un régimen de temperaturas negativas. Podemos ver
además que la aproximación no es muy buena para 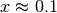 [1]. ¿Cuándo comienzan las temperaturas negativas? Cuando se
anula el argumento del logaritmo, es decir
[1]. ¿Cuándo comienzan las temperaturas negativas? Cuando se
anula el argumento del logaritmo, es decir
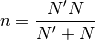
Ensamble canónico¶
Resolvamos ahora este problema en el ensamble canónico, suponiendo que
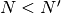 .
.
(6)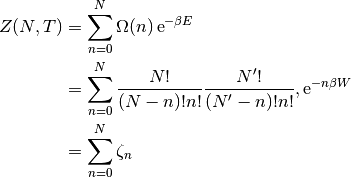
Esta suma no parece nada fácil de calcular, así que vamos a ver cómo
la podemos aproximar. Vamos a gráficar  para
para 
import numpy as np
import pylab as pl
from scipy.misc import comb, factorial
N = 500
n = np.linspace(0,N, N+1)
x = n/N
z = comb(N, n)**2 * np.exp(-n)
pl.figure()
pl.plot(x, z)
pl.title(r'Secuencias de la funcion de particion para N={0}'.format(N))
pl.xlabel(r'$x = n/N$')
pl.ylabel(r'$\zeta(n)$')
pl.tight_layout()
(Source code, png, hires.png, pdf)
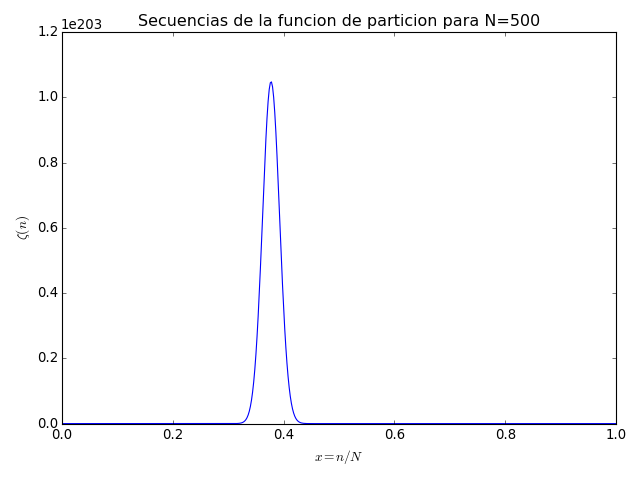
Vemos que hay claramente un máximo, y tiene una forma de campana. Por
lo pronto, entonces, vamos a tratar de aproximarla por una
gaussiana. Para eso, analicemos los términos que la componen,
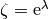
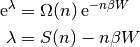
El máximo de 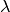 se da para
se da para
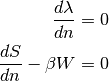
Utilizando (2) y (3), podemos hallar la derivada de la entropía. De esta manera, el máximo se da en
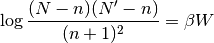
A partir de aquí vamos a analizar (para que las cuentas sean más
sencillas) el caso 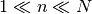 [2]. Así, resulta
[2]. Así, resulta
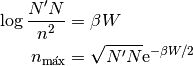
Y la derivada segunda en el máximo es
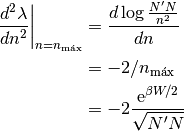
Tenemos entonces, a orden 2 en Taylor, la expresión de los términos de la suma:
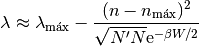
Volviendo a la expresión original, (6),
(7)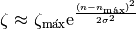
con
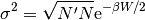
Bueno, entonces, ¿para qué dimos tantas vueltas? En la ecuación (7) aproximamos la función de partición cerca del máximo como una distribución gaussiana. Podemos calcular la sumatoria como el área bajo esta gaussiana:
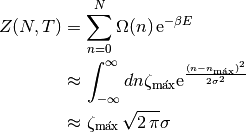
Recordemos que al fin y al cabo, lo único que nos importa en la termodinámica es el logaritmo de la función de partición:
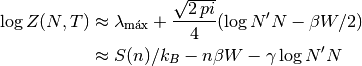
Como 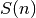 y
y 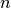 son variables extensivas, crecen mucho
más rápido que cualquier término
son variables extensivas, crecen mucho
más rápido que cualquier término 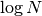 , por lo que
, por lo que
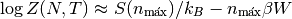
Con buen tino pueden pensar que hicimos demasiadas aproximaciones como
para que esto sea verdad. Vamos a ver el caso general. Queremos
estudiar específicamente cuál es el error relativo que obtenemos en la
termodinámica al aproximar 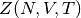 por
por
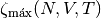 . Como ya dijimos, en la
termodinámica nos interesan los logaritmos, por lo que queremos
calcular entonces
. Como ya dijimos, en la
termodinámica nos interesan los logaritmos, por lo que queremos
calcular entonces
(8)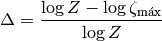
Partimos entonces de la expresión de la función de partición
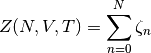
Como regla general, vale
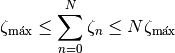
Tomemos logaritmo de la expresión anterior, y obtenemos
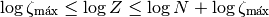
Y ahora restamos 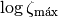 , para acercarnos a
la expresión (8):
, para acercarnos a
la expresión (8):
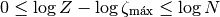
Finalmente, nosotros sabemos que estamos tratando sistemas
termodinámicos. De ese modo, sabemos que 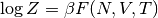 . Como
. Como 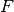 es un potencial termodinámico, es homogéneo de
primer orden y vale
es un potencial termodinámico, es homogéneo de
primer orden y vale 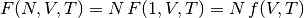 . Así, dividiendo por
. Así, dividiendo por 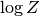 la expresión anterior tenemos
la expresión anterior tenemos
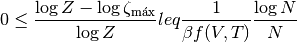
Usando (8),
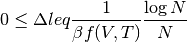
y, entonces, en el límite 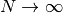 ,
,
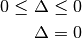
| [1] | De todos modos, para valores típicos de 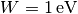 , , 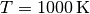 y y 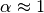 , resulta , resulta 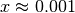 |
| [2] | El razonamiento vale igual para los otros casos, pero las cuentas se vuelven engorrosas. Pero pronto vamos a ver que no importa exactamente la forma de la función de partición. |