Problema 4: Dos niveles¶
Sea un sistema de partículas distinguibles y no interactuantes, cada una
de las cuales puede tener dos valores de energía,  y
y
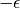 .
.
- Suponiendo que dicho sistema está aislado y consiste de
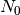 partículas con una energía total
partículas con una energía total 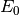 , calcule
su entropía suponiendo
, calcule
su entropía suponiendo 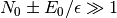
Calcular la entropía para un sistema es simplemente contar la cantidad
de estados compatibles 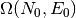 :
:
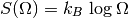
Tenemos entonces que hallar la cantidad de estados compatibles con una
energía 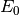 . Para eso calculamos la energía y el total de
partículas para un sistema con
. Para eso calculamos la energía y el total de
partículas para un sistema con 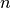 partículas en el estado
partículas en el estado
 y
y 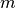 partículas en el estado
partículas en el estado 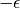 :
:
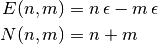
Ahora usamos los dos vínculos que tiene el ensamble microcanónico:
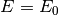 ,
, 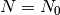 :
:
(1)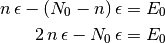
De este modo queda claro que elegir 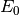 es elegir, de las
es elegir, de las
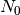 partículas, la cantidad de partículas
partículas, la cantidad de partículas 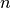 tal que
tal que
(2)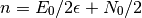
Esto es claramente un número combinatorio:
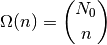
(3)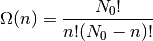
y, en consecuencia:
(4)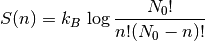
Particularmente, en el caso en que 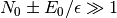 ,
a partir de (2), vemos que tanto
,
a partir de (2), vemos que tanto 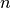 como
como 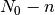 son números muy grandes:
son números muy grandes:
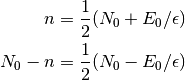
Así, podemos usar la aproximación de Stirling en (3)
![S(n) \approx S_S(n) = k_B\,[N_0 \log N_0 - N_0 - n \log n + n - (N_0 - n) \log (N_0 - n) + (N_0 - n)]](../../_images/math/4a09456b83fc21e443ecc25a6f12ceafd5c1fa3c.png)
y, simplificando, con 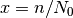 (ver Apéndice).
(ver Apéndice).
(5)![S_S(x) = N_0\,k_B\,[- x \log x - (1 - x) \log (1 - x)]](../../_images/math/4370073e2befac39f70fd7b25a8a167873c50139.png)
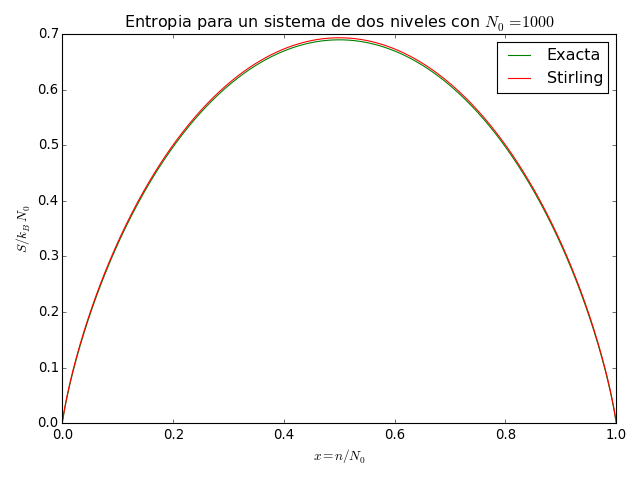
Los gráficos de la entropía, de acuerdo a (5) y (4)
(para 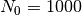 ) son:
) son:
import numpy as np
import pylab as pl
from scipy.misc import comb
N0 = 1000
n = np.linspace(0, N0, N0+1)
x = n/N0
S = np.log(comb(N0, n))/N0
Ss = - x * np.log(x) - (1 - x) * np.log(1 - x)
pl.figure()
pl.plot(x, S, 'g-', label='Exacta')
pl.plot(x, Ss, 'r-', label='Stirling')
pl.xlabel(r'$x = n/N_0$')
pl.ylabel(r'$S/k_BN_0$')
pl.title(r'Entropia para un sistema de dos niveles con $N_0 = {0}$'.format(N0))
pl.tight_layout()
pl.legend()
(Source code, png, hires.png, pdf)
A partir de la entropía podemos hallar la temperatura, sabiendo que
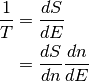
Hallar la derivada de 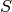 respecto de
respecto de 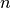 puede parecer
extraño, pero es aún más sencillo:
puede parecer
extraño, pero es aún más sencillo:
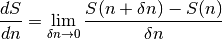
En este caso, el límite es una diferencia finita, con
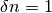 . Reemplazando, obtenemos
. Reemplazando, obtenemos
![\frac{1}{T} &= \left[S(n+1) - S(n)\right] \,\frac{d}{dE}(E/2\epsilon + N_0/2)\\
&= k_B [\log\Omega(n+1) - \log\Omega(n)] \,\frac{1}{2\epsilon}](../../_images/math/134563497eb4076f05c2791af3f4fc45b565536c.png)
Y llegamos a un resultado mucho más lindo:
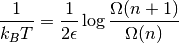
Con la expresión de 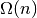 hallamos
hallamos
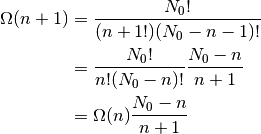
La temperatura entonces es:
(6)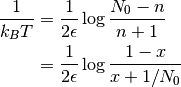
Mediante la aproximación de Stirling, derivando (5),
obtenemos (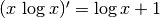 )
)
![\frac{1}{k_BT}&= \frac{1}{2\epsilon}[-\log{x} + \log{1-x}]\\
&= \frac{1}{2\epsilon}\log\frac{1-x}{x}\\](../../_images/math/944941bb581a21c84d7eaf2fea23628ca4b0cd57.png)
import numpy as np
import pylab as pl
from scipy.misc import comb
N0 = 1000
x = np.linspace(0, 1, N0+1)
T = 1/np.log((1-x)/(x+1/N0))
pl.figure()
pl.plot(x, T, 'g-')
pl.plot([0.5, 0.5], [-50, 50], 'k--')
pl.xlabel(r'$x = n/N_0$')
pl.ylabel(r'$k_BT/2\epsilon$')
pl.ylim((-50, 50))
pl.title(r'Temperatura para un sistema de dos niveles con $N_0 = {0}$'.format(N0))
pl.tight_layout()
(Source code, png, hires.png, pdf)
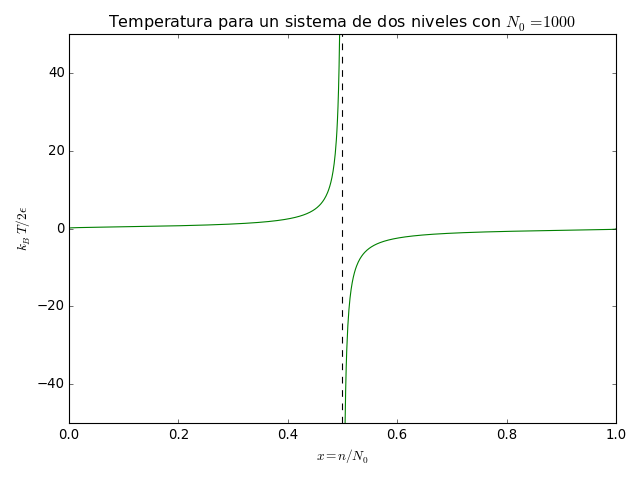
En este gráfico podemos notar que la temperatura toma valores
negativos para 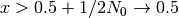 . Si no se
sorprendieron es porque, o bien no tienen alma, o porque ya sabían el
resultado. Este resultado es, de hecho, bastante común en sistemas con
espectros de energía acotado. El motivo surge de lo siguiente: a
diferencia de lo que sucede en el gas ideal, en este caso la entropía
no siempre es una función creciente de la energía. Esto es porque, a
medida que tenemos más energía, nos quedan pocas formas de elegir los
microestados que corresponden al estado macroscópico (llegando al
extremo de
. Si no se
sorprendieron es porque, o bien no tienen alma, o porque ya sabían el
resultado. Este resultado es, de hecho, bastante común en sistemas con
espectros de energía acotado. El motivo surge de lo siguiente: a
diferencia de lo que sucede en el gas ideal, en este caso la entropía
no siempre es una función creciente de la energía. Esto es porque, a
medida que tenemos más energía, nos quedan pocas formas de elegir los
microestados que corresponden al estado macroscópico (llegando al
extremo de 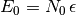 , donde hay un solo microestado
compatible: todas las partículas en
, donde hay un solo microestado
compatible: todas las partículas en  ). Incluso más,
cuando
). Incluso más,
cuando 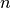 pasa el valor 0.5, la temperatura salta abruptamente
desde
pasa el valor 0.5, la temperatura salta abruptamente
desde 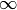 a
a 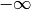 [1]. La única forma
sensata de entender esto es a las temperaturas negativas como “más
caliente” que las positivas. Es decir, el calor fluye de las
temperaturas negativas hacia las positivas.
[1]. La única forma
sensata de entender esto es a las temperaturas negativas como “más
caliente” que las positivas. Es decir, el calor fluye de las
temperaturas negativas hacia las positivas.
(b) Suponga ahora que el sistema de 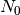 partículas es cerrado
y su energía media vale
partículas es cerrado
y su energía media vale 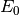
- Calcule su temperatura y el rango de
en la que es positiva
- Calcule la entropía y compare con la calculada en (a).
En este caso tendremos que usar el ensamble canónico. Para eso tenemos que calcular la función de partición:
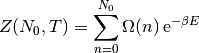
Utilizando la expresión 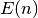 de (1) y
de (1) y 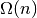 de (3), queda
de (3), queda
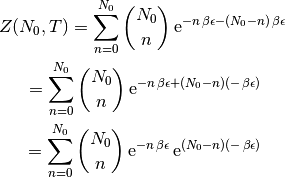
Esta expresión es el binomio de Newton, y
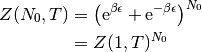
que no es más que el resultado que ya conocemos, que la función de partición es separable para las partículas cuando éstas son independientes [2].
Ahora podemos calcular la energía libre de Helmholtz
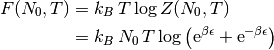
y la energía media:
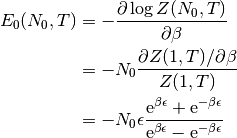
Tenemos que despejar la temperatura de esta expresión, pero es más
fácil de lo que parece. Si definimos 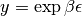 ,
,
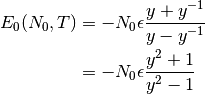
Reemplazando 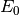 con su espresión para
con su espresión para 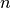 de acuerdo a
(1):
de acuerdo a
(1):
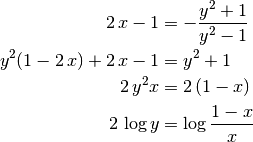
y ahora reemplazando 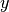 , llegamos a
, llegamos a
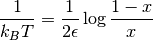
que, en el límite termodinámico, es exactamente la misma expresión que obtuvimos anteriormente en (6). Es decir, se mantiene la equivalencia entre ensambles. Que aparezcan temperaturas negativas no tiene que ver con el ensamble utilizado. Vamos a verlo nuevamente, ahora en el gran canónico:
(c) Finalmente suponga que el sistema es abierto con un número medio
de partículas 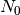 y una energía media
y una energía media 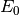 .
.
Calcule
como función de la temperatura y del número medio de partículas. Compare con los resultados anteriores.
Generalice el resultado anterior demostrando que para un sistema formado por elementos independientes y distinguibles, existe la siguiente relación entre los ensambles canónico y gran canónico:
donde
es la energía por elemento.
En esta situacíon tendremos que usar el ensamble gran canónico, con la ¿gran función de partición?, ¿función de gran partición?, ¿función de partición grande?:
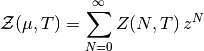
con 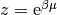 la fugacidad. En el caso en el que
las partículas son independientes, como
la fugacidad. En el caso en el que
las partículas son independientes, como 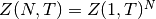 ,
la función de partición GC es
,
la función de partición GC es
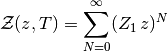
Y esto es una serie geométrica,
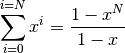
Usando el límite 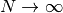 (¡si
(¡si 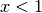 !), la
función de partición GC resulta
!), la
función de partición GC resulta
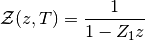
Para calcular el número medio de partículas,
(7)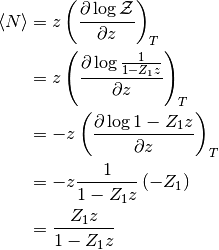
Y para la energía interna
(8)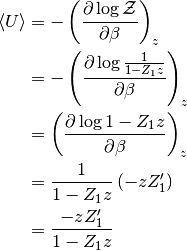
Y si dividimos la ecuación (8) por (7), se simplifica todo
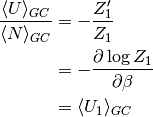
que demuestra el punto ii y, en consecuencia, el punto i.
| [1] | En realidad, 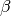 pasa suavemente por el 0,
cambiando de signo. Al fin y al cabo, ¿qué tiene de
interesante la temperatura? ¿No podemos hablar siempre de pasa suavemente por el 0,
cambiando de signo. Al fin y al cabo, ¿qué tiene de
interesante la temperatura? ¿No podemos hablar siempre de
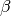 ? ? |
| [2] | En el caso en el que son indistinguibles, aparece el “factor
de buen conteo” 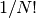 |