and Q) involved in the fast reactions, while there are other N
( 
, where N might equal zero) that are not. The spatio-temporal variation
of the various concentrations is described by a set of n+N+1
reaction-diffusion equations of the form:
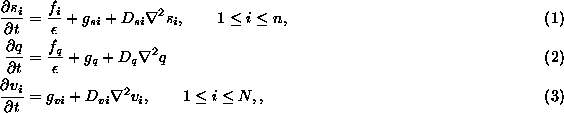
which are to be solved subject to boundary and initial conditions for 
, 
and 
. In (1)-(3),
,
,
, 
, 
and 
are the concentrations and diffusion coefficients of the n+N+1
species, 
( 
), Q and 
( 
), respectively. 
, 
, 
, 
and 
are functions of the concentrations:
and
do not depend on 
, but
,
and
may depend on any of the concentrations, including
. These functions model the variation of the concentrations due to the
chemical reactions and to the external feed or removal of each species.
The f terms only include the fast reactions while both the slow
reactions, the feed and the removal are included in the g terms.
We make the difference between the two timescales explicit by introducing
the small parameter, 
, which is of the order of the ratio between the timescales. Q is
any species involved in the fast reaction whose concentration varies because
of it (see later). In the case with more fast reactions, we separate as
many species, 
, as fast reactions, whenever that is possible.
The aim of the calculation is to obtain a reduced set of differential
equations which describe the evolution on the slow timescale dynamics.
The differential equations that are ``eliminated'' are actually replaced
by algebraic relations among the concentrations. In the case of one fast
reaction the system is finally described by n+N differential
equations and one algebraic relation of the form 
. In the general case of 
fast reactions ( 
), up to
differential equations can be replaced by algebraic relations (provided
that the number of species involved in the fast reactions is larger than
).
We will do the calculation for the case of only one fast reaction, discussing two subcases. First, the case of one fast reversible reaction, which we write as:
where 
and 
stands for the stoichiometric coefficients of the reactants and products
respectively and we have made the existence of two timescales explicit
by the introduction of the small number
in the reaction rates. The second subcase corresponds to a situation in
which there is one fast irreversible reaction of the form (4)
but with k'=0.
As usual, we describe the chemical reaction by mass action kinetic equations.
Thus the terms with
and
in Eqs. (1)-(2)
can be written as:
The functions
and
are then related by:
The condition on Q mentioned before is equivalent to saying that 
. In this way, as required, the concentration of Q varies due to
the fast reaction.
