and 
. We introduce this rescaling explicitly so that both T and 
are quantities of order one. We then assume that the concentrations of
the species involved in the fast reaction depend on these two time variables, 
, 
,
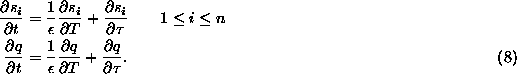
while the rest of the concentrations, 
, 
, only depend on the slow time variable,
. In this way, the time derivatives of the s and q concentrations
are given by
We also expand the s and q concentrations as:
Inserting Eqs. (8) and (9)
in Eqs. (1)-(2)
and equating terms with equal powers of 
we find:
To 
:
To 
:
Using relation (7) we can rewrite Eqs. (10)-(13) as:
for 
.
As mentioned before, in principle, 
(
) and q depend on both T and
. However, due to the separation of timescales, we can first integrate
the equations in T treating
as an independent variable that is held constant .
We do that with Eqs. (14)-(15),
which then can be treated as a set of n+1 ordinary differential
equations. The solutions will be of the form:
where 
corresponds to a fixed point solution of the set (14)-(15),
i.e., they satisfy:
with 
(
) and 
independent of T. From (20) we expect
to find algebraic relations of the form
that define n-dimensional sets of fixed points in the (n+1)-dimensional
space of concentrations, 
. Here the main difference between the cases of reversible and irreversible
reactions arises. In the case of one reaction of the form (4)
with 
we obtain only one relation given by:
On the other hand, if k'=0, then (20)
implies that at least one concentration, 
, is equal to zero. We schematically depict both situations in Figs. 1
(a) and (b), where we have plotted the surfaces determined by condition
(20) in the case of three species, 
, 
and Q.
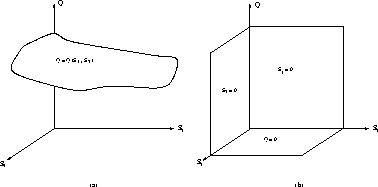
Figure: (a) Manifold defined by the algebraic relation (22)
in the case of one fast reversible reaction involving three species,
,
and 
. (b) Similar to (a) but for one irreversible reaction involving
,
and Q. In this case three surfaces of fixed points for the fast
dynamics exist: 
, 
and Q=0.
We discuss the
case first. Since there are no feeding terms in Eqs. (14)-(15),
we expect the dynamical system (14)-(15)
to be dissipative. Therefore, we expect the existence of attractors. On
the other hand, as shown in Sec. III, due to the existence of several constants
of motion, the only possible attractors are fixed points. In particular,
we assume that all the fixed points defined by (21)
are stable .
Then, for almost every initial condition, the functions 
and 
will become negligible in front of
and
, respectively, as T increases. Which fixed point on the N-dimensional
space defined by (20) is initially approached
depends on the initial condition (see Sec. III). Given one initial condition,
the system approaches very fast (on the fast timescale) this initial ``fixed
point'', which is actually a fixed point for the fast timescale dynamics.
Then, the slow dynamics moves the system on the N-dimensional space
defined by (20). In other words, on the fast
timescale, the concentrations
and q approach the slowly varying functions
and
. These are the slowly varying portions of the concentrations that we are
interested in. The algebraic relation (21)
implies that 
depends on
(and 
) through the
(and
) dependence of the concentrations 
,..., 
. It also means that not all of the slowly varying concentrations are independent,
and this allows the reduction of the number of relevant dynamic equations.
We now turn to Eqs. (16)-(17).
Replacing the solutions (18)-(19)
and neglecting the terms 
and 
in front of
and
respectively, we find:
where the partial derivatives 
,
, 
and
must be evaluated at the fixed point 
, and
should be written as a function of 
using relation (21) ((22)
in our case).
So far we have not talked about the evolution equations for the v
concentrations. Inserting the solutions (18)-(19)
in (3) and neglecting the terms
and
in front of
and
as before, the form of Eqs. (3) remains
the same, with the only difference that
and q are to be replaced by
and
. This is consistent with our previous assumption that the v concentrations
only vary on the slow timescale,
. In this way, all the terms on the right-hand-side of Eqs. (23)-(24)
only depend on
, while the ones on the left-hand-side depend both on
and T. Thus, these equations can be separated in two parts:
and
with 
and 
unknown functions of
.
In order to get rid of these unknown functions, we multiply each of
Eqs. (23) by 
and subtract Eq. (24). We get n
equations of the form:
As before, these equations can be separated in two:
with 
. These functions of
must be treated as constants when solving Eqs. (25)-(26).
From Eq. (30) we see that if 
is different from zero, then 
will grow linearly in time with T. In this way this difference will
become too large, breaking up the asymptotic expansion (9).
Therefore, the only way to keep this expansion well-behaved it is to set 
for al .
We have the freedom to do it. In this way we guarantee that the solutions
of Eqs. (25)-(26),
on the fast timescale, approach slowly varying functions of time that remain
bounded for all times so that 
and 
. This let us conclude that
Setting
also leaves us with a closed set of n+N differential equations
for the slowly varying concentrations
,
and
,
. Namely, we obtain the n equations for
inserting the algebraic relation (21)
in (31). They read:
for
, with
given by (22). In particular, from (22)
we obtain that:
Inserting (35) in (34) we obtain the equations:
which must be solved coupled to Eqs. (3)
with 
. As shown in Sec. III, given initial conditions for Eqs. (1)-(3)
we can determine unique values for 
(
) and 
that satisfy the relation (21). These,
together with 
, are the initial conditions for the reduced set of equations.
We now repeat the calculation in the case of one fast irreversible reaction,
i.e., when 
and 
are of the form (5)-(6)
with k'=0. We introduce the two time variables, T and
, and the expansion (9) getting Eqs.
(10)-(13)
as before. But now, when we look for fixed point solutions of the ``fast''
system (10)-(11)
we observe that there are n+1 n-dimensional sets of fixed
points defined by 
, 
,..., 
or q=0. As explained in Sec. III, if the dynamics is dissipative,
then there are always stable fixed points in some of those sets. As in
the
case, given an initial condition for the system (10)-(11),
there is a unique stable fixed point that the system approaches eventually
in time. Without loss of generality let us call Q the species for
which the concentration is zero at this attracting fixed point (clearly 
for the concentration to decrease in time from a positive value to zero).
Then, as before the solutions of (10)-(11)
are of the form (18)-(19),
but now 
. This implies that 
, at the fixed point 
, 
, while 
at the fixed point, unless 
, in which case it is 
. Therefore, instead of Eqs. (23)-(24),
we get in this case:
if
, and
if 
. The
case can be handled as before, yielding the reduced equations:
On the other hand, in the
case, if 
, Eq. (40) implies that 
varies linearly with T and this breaks down the asymptotic expansion
we are assuming. Therefore, we can separate the two timescales for the
k'=0,
case as before only if 
, getting the reduced equations:
In certain cases, a similar (but more complicated) calculation can be done if there is more than one fast reaction. Depending on the number of fast reactions and on the number of species involved, as many variables as fast reactions can be eliminated by this procedure. However, this is not always possible to accomplish and the situation has to be analyzed on a one by one basis.
