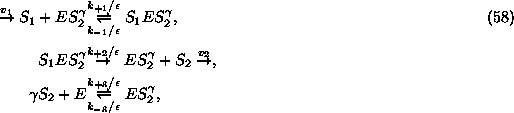
 represents an open monosubstrate and monoproduct reaction catalized by
an allosteric enzyme which is inhibited by the substrate and activated
by the product. The model describes the kinetics of the reactions involved
in the appearance of a single frequency oscillation in the glycolytic pathway.
The simple kinetic model developed by Selkov reads:
represents an open monosubstrate and monoproduct reaction catalized by
an allosteric enzyme which is inhibited by the substrate and activated
by the product. The model describes the kinetics of the reactions involved
in the appearance of a single frequency oscillation in the glycolytic pathway.
The simple kinetic model developed by Selkov reads:
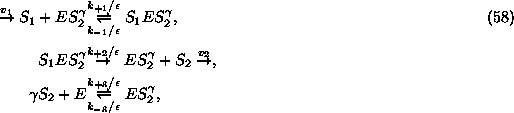
where ![]() is supplied by an external source at the rate
is supplied by an external source at the rate ![]() which is supposed to remain constant during the reaction. From the equations
it is clear that
which is supposed to remain constant during the reaction. From the equations
it is clear that ![]() is irreversibly converted into the product molecules
is irreversibly converted into the product molecules ![]() . The product is then removed by an irreversible sink at the rate
. The product is then removed by an irreversible sink at the rate ![]() . The free enzyme E is inactive unless when it has
. The free enzyme E is inactive unless when it has ![]() product molecules bounded, forming the complex
product molecules bounded, forming the complex ![]() . Assuming that the sink of the product behaves as a first order reaction,
and including in the description the transport of the substrate and product
molecules by diffusion (the transport of the enzyme and its complexes can
be neglected) the reaction-diffusion system can be written as:
. Assuming that the sink of the product behaves as a first order reaction,
and including in the description the transport of the substrate and product
molecules by diffusion (the transport of the enzyme and its complexes can
be neglected) the reaction-diffusion system can be written as:
where
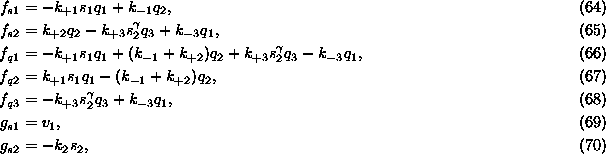
with ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Adding Eqs. (61), (62)
and (63), the constancy of the total
amount of the enzyme becomes evident:
. Adding Eqs. (61), (62)
and (63), the constancy of the total
amount of the enzyme becomes evident: ![]() . That allows us to reduce the dimensionality of the system by one.
. That allows us to reduce the dimensionality of the system by one.
According to Selkov's data, the concentration of E and its complexes
is 3 to 4 orders of magnitude below those of ATP and ADP.
So, we can rescale the ![]() concentrations by a small parameter (of the order of
concentrations by a small parameter (of the order of ![]() ), as done in
), as done in  .
In order to discuss the validity of the approximation in different limits
we will introduce a new parameter
.
In order to discuss the validity of the approximation in different limits
we will introduce a new parameter ![]() such that
such that ![]() and
and ![]() and use the expansion
and use the expansion ![]() to simplify the notation.
to simplify the notation.
We proceed as described in Sec. V of the paper in order to get rid of ![]() ,
, ![]() and
and ![]() in favor of
in favor of ![]() and
and ![]() . The set of algebraic relations
. The set of algebraic relations ![]() can be solved. Its solutions are given by
can be solved. Its solutions are given by
where we have defined the rescaled concentrations, ![]() and
and ![]() , as
, as
In this case, as we are dealing with more than one fast reaction, the
equations for the first correction terms, ![]() , can be written together in matrix form. Their expression reads,
, can be written together in matrix form. Their expression reads,
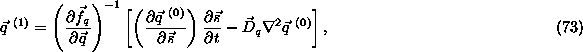
from which we get:
where ![]() .
.
Introducing the expansions ![]() , with
, with ![]() and
and ![]() given by Eqs. (71) and (74),
into Eqs. (59)-(60),
and using the rescaled variables (72) we
finally find:
given by Eqs. (71) and (74),
into Eqs. (59)-(60),
and using the rescaled variables (72) we
finally find:
where we have defined